/Szkoła średnia/Liczby/Liczby całkowite/Podzielność/1 literka

Zadanie nr 6198174

Dodaj do ulubionych
Dodaj do rozwiązanych

Uzasadnij, że dla każdej liczby całkowitej 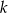k liczba 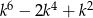6 4 2 k − 2k + k jest podzielna przez 36.

Rozwiązanie

Sposób I

Zauważmy, że

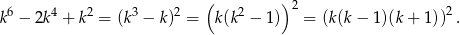
6 4 2 3 2 ( 2 )2 2 k − 2k + k = (k − k) = k(k − 1) = (k (k− 1 )(k+ 1 )) .

Wystarczy zatem wykazać, że liczba 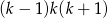(k − 1)k(k + 1) jest podzielna przez 6. To jest jednak oczywiste: jest to iloczyn trzech kolejnych liczb całkowitych, więc jedna z tych liczb jest podzielna przez 3, i co najmniej jedna z nich jest parzysta. Iloczyn jest więc podzielny przez 6.

Sposób II

Zauważmy, że

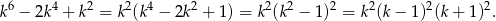
k6 − 2k4 + k2 = k2(k4 − 2k2 + 1) = k2(k2 − 1)2 = k2(k − 1)2(k + 1)2.

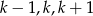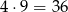Zauważmy teraz, że liczby k − 1 ,k ,k + 1 są kolejnymi liczbami całkowitymi, więc przynajmniej jedna z nich jest parzysta. Kwadrat tej liczby będzie więc podzielny przez 4. Jedna z tych liczb musi też być podzielna przez 3 (być może ta sama, która była parzysta), kwadrat tej liczb jest podzielny przez 9. Cały iloczyn jest więc podzielny przez 4 ⋅9 = 3 6 .

Wersja PDF