Zadanie nr 6340692
Udowodnij, że dla każdej liczby całkowitej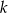 
i dla każdej liczby całkowitej 
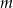liczba 
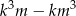jest podzielna przez 6.
Rozwiązanie
Zauważmy, że
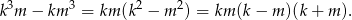
Widać teraz, że liczba ta jest parzysta, bo albo jedna z liczb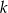 
lub 
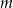jest parzysta, albo 
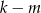jest parzyste.
Liczba ta dzieli się też przez 3, bo albo jedna z licz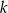b 
lub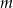 
dzieli się przez 3, albo liczby te dają te same reszty z dzielenia przez 3 i wtedy 
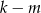dzieli się przez 3, albo wreszcie 
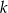i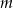 
dają różne niezerowe reszty z dzielenia przez 3, czyli dają reszty 1 i 2 (lub odwrotnie) – wtedy 
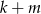dzieli się przez 3.
