/Szkoła średnia/Funkcje/Kwadratowa/Wyznacz wzór

Zadanie nr 4637852

Dodaj do ulubionych
Dodaj do rozwiązanych

Funkcja kwadratowa 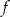f określona jest wzorem 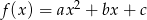2 f (x) = ax + bx + c . Zbiorem rozwiązań nierówności 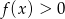f (x) > 0 jest przedział 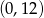(0,12 ) . Największa wartość funkcji 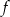f jest równa 9. Oblicz współczynniki a,b i c funkcji f .

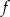Rozwiązanie

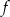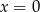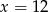Z podanych informacji wiemy, że wykresem funkcji f jest parabola o ramionach skierowanych w dół, miejscach zerowych x = 0 i x = 12 , oraz wierzchołku w punkcie 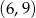(6,9) (bo wierzchołek musi być dokładnie w środku między pierwiastkami).

Sposób I

Skoro znamy współrzędne wierzchołka, to wiemy, że funkcja 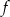f ma wzór postaci

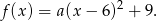
2 f (x) = a(x − 6) + 9.

Wiemy ponadto, że 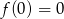f(0) = 0 , więc

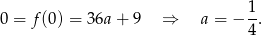
0 = f (0) = 36a + 9 ⇒ a = − 1. 4

Stąd

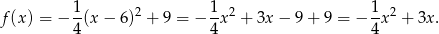
1 1 1 f(x ) = − -(x − 6)2 + 9 = − -x2 + 3x − 9 + 9 = − -x2 + 3x. 4 4 4

Sposób II

Korzystając z podanych miejsc zerowych, mamy

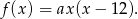
f (x) = ax (x− 12).

Teraz podstawiamy w tym wzorze współrzędne wierzchołka.

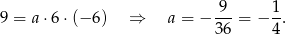
9 1 9 = a⋅6 ⋅(− 6) ⇒ a = − ---= − -. 36 4

Zatem

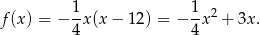
1 1 2 f (x) = − 4x (x− 12) = − 4-x + 3x.

Na koniec wykres funkcji f dla ciekawskich.

PIC

 
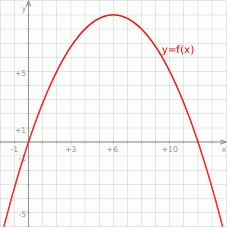
Odpowiedź: ( ) (a,b,c) = − 1,3,0 4

Wersja PDF