/Szkoła średnia/Geometria/Planimetria/Trójkąt

Zadanie nr 2440248

Dodaj do ulubionych
Dodaj do rozwiązanych

Podstawa 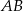AB trójkąta równoramiennego 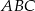ABC ma długość 8 oraz 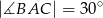|∡BAC | = 30∘ . Oblicz długość środkowej 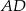AD tego trójkąta.

Rozwiązanie

Sposób I

Rozpoczynamy oczywiście od rysunku.

PIC

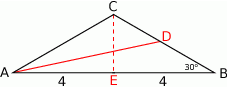
Z trójkąta prostokątnego 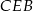CEB wyliczamy długość ramienia.

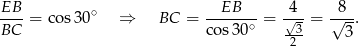
EB EB 4 8 ---= cos 30∘ ⇒ BC = -------= √-- = √--. BC cos30 ∘ -23 3

Zatem 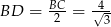BD = BC-= √4- 2 3 i długość odcinka 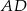AD możemy wyliczyć z twierdzenia cosinusów.

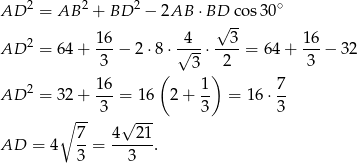
2 2 2 ∘ AD = AB + BD − 2AB ⋅ BD√ co s30 2 16 4 3 16 AD = 64 + ---− 2 ⋅8⋅ √---⋅----= 64+ ---− 32 3 ( 3 ) 2 3 2 16- 1- 7- AD = 32 + 3 = 16 2+ 3 = 16 ⋅3 ∘ -- √ --- 7- 4--21- AD = 4 3 = 3 .

Sposób II

Tym razem dorysujmy punkt 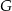G w ten sposób, by odcinek 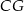CG był równoległy do 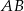AB , a odcinek 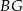BG równoległy do AC .

PIC

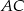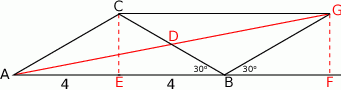
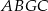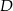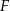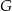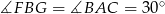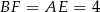Otrzymaliśmy w ten sposób równoległobok ABGC . Ponieważ przekątne równoległoboku dzielą się na połowy, punkt D jest punktem przecięcia się jego przekątnych. Ponadto, jeżeli F jest spodkiem wysokości opuszczonej z wierzchołka G to ∡F BG = ∡BAC = 30∘ oraz BF = AE = 4 . Mamy zatem

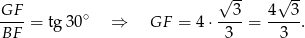
√ -- √ -- GF--= tg30∘ ⇒ GF = 4 ⋅--3-= 4--3. BF 3 3

Stąd

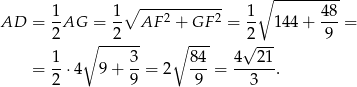
∘ ------------ ∘ --------- AD = 1AG = 1- AF 2 + GF 2 = 1- 144 + 4-8 = 2 --2--- --- 2 9 1 ∘ 3 ∘ 84 4 √ 21- = -⋅ 4 9 + --= 2 ---= ------. 2 9 9 3

 
Odpowiedź: 4√-21 AD = 3

Wersja PDF