Zadanie nr 4957490
Wykaż, że jeśli 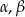 są kątami ostrymi trójkąta prostokątnego, to
są kątami ostrymi trójkąta prostokątnego, to 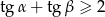 .
.
Rozwiązanie
Sposób I
W trójkącie prostokątnym 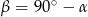 , więc
, więc
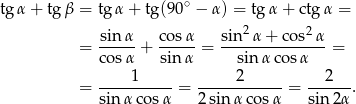
Zauważmy teraz, że jeżeli 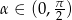 to
to 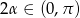 . Zatem
. Zatem
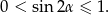
Mamy stąd
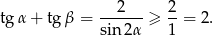
Sposób II
Narysujmy trójkąt prostokątny o przyprostokątnych  i
i 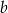 .
.
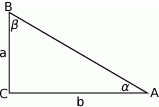
Przy tych oznaczeniach mamy
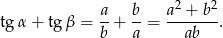
Pozostało więc wykazać, że
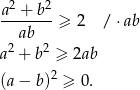
Otrzymana nierówność jest oczywiście prawdziwa, a przekształcaliśmy w sposób równoważny, więc wyjściowa nierówność też musiała być prawdziwa.

