Zadanie nr 9148281
Oblicz sinusy kątów ostrych trójkąta prostokątnego, wiedząc, że stosunek długości promienia okręgu wpisanego do promienia okręgu opisanego na tym trójkącie jest równy 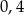 .
.
Rozwiązanie
Rozpoczynamy od rysunku.
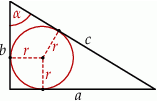
Sposób I
Promień okręgu opisanego na trójkącie prostokątnym to połowa przeciwprostokątnej (bo jest ona średnicą okręgu opisanego). Zatem 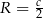 . Promień okręgu wpisanego obliczamy ze wzoru na pole.
. Promień okręgu wpisanego obliczamy ze wzoru na pole.
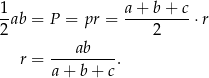
Mamy zatem
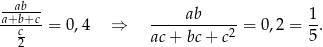
Podzielimy teraz licznik i mianownik przez 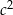 , tak aby móc skorzystać z równości
, tak aby móc skorzystać z równości 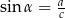 i
i 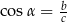 .
.
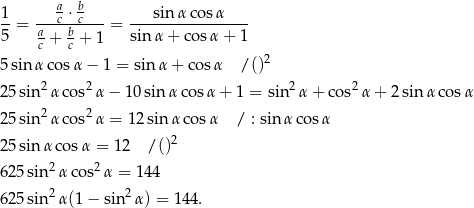
Podstawiamy teraz 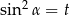 i mamy
i mamy
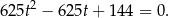
Liczymy
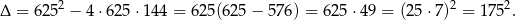
Stąd 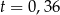 lub
lub 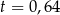 , czyli
, czyli 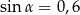 lub
lub 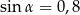 .
.
Sposób II
Wiemy, że przeciwprostokątna trójkąta prostokątnego jest dwa razy dłuższa od promienia okręgu opisanego, więc
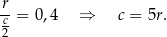
Stąd
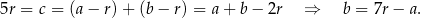
Udało nam się więc wyrazić długości wszystkich trójkąta w zależności od  i
i  .
.
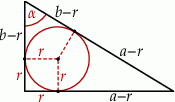
Piszemy teraz twierdzenie Pitagorasa.
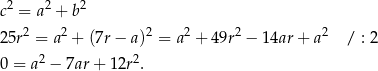
Traktujemy  jak parametr i rozwiązujemy otrzymane równanie kwadratowe.
jak parametr i rozwiązujemy otrzymane równanie kwadratowe.
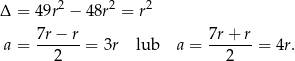
Interesujące nas sinusy kątów ostrych są więc równe
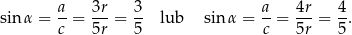
Sposób III
Tak jak w poprzednim sposobie dochodzimy do równości
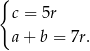
Podnosimy teraz drugą z tych równości do kwadratu i korzystamy z twierdzenia Pitagorasa.
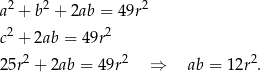
Mamy zatem układ równań
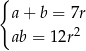
Możemy go rozwiązać, ale tak naprawdę nie potrzebujemy wartości  i
i 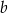 , ale sinusy, czyli liczby
, ale sinusy, czyli liczby  i
i 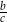 . Dzielimy zatem pierwsze równanie przez równość
. Dzielimy zatem pierwsze równanie przez równość 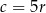 , a drugie przez
, a drugie przez 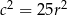 i mamy układ
i mamy układ
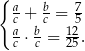
Na mocy wzorów Viète’a oznacza to, że szukane sinusy są pierwiastkami równania kwadratowego
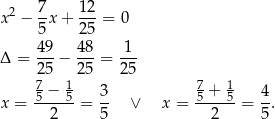
Sposób IV
Oznaczmy długość odcinka łączącego środek przeciwprostokątnej z punktem styczności okręgu z przeciwprostokątną przez  .
.
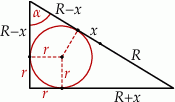
Wiemy, że 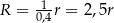 , zatem przyprostokątne mają odpowiednio długości
, zatem przyprostokątne mają odpowiednio długości
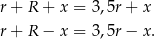
Pozostało teraz napisać twierdzenie Pitagorasa.
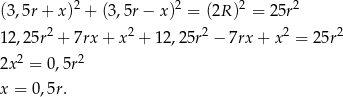
Zatem szukane sinusy to
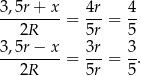
Sposób V
Tym razem skorzystamy ze wzoru
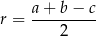
na promień okręgu wpisanego w trójkąt prostokątny. Mamy więc
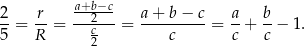
Zauważmy, że ułamki, które otrzymaliśmy z prawej strony to dokładnie funkcje trygonometryczne kąta  .
.
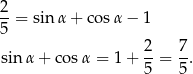
Podniesiemy teraz tę równość do kwadratu, aby móc skorzystać z jedynki trygonometrycznej.
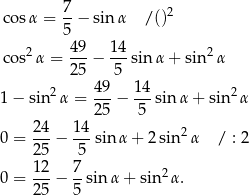
Podstawiamy teraz 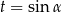 i mamy równanie
i mamy równanie
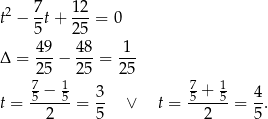
Zatem 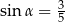 lub
lub 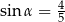 .
.
Sposób VI
Tak samo jak w pierwszym sposobie dochodzimy do równości 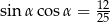 . Tym razem jednak skorzystamy ze wzorów na
. Tym razem jednak skorzystamy ze wzorów na 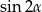 i
i 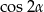 .
.
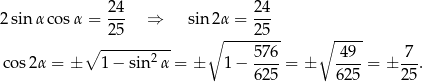
Zauważmy, że wprawdzie  jest kątem ostrym, ale
jest kątem ostrym, ale 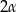 już ostry być nie musi – dlatego właśnie nie możemy założyć, że
już ostry być nie musi – dlatego właśnie nie możemy założyć, że 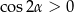 . Mając obliczony
. Mając obliczony 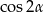 , możemy obliczyć
, możemy obliczyć 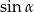 ze wzoru
ze wzoru
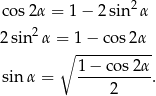
( jest kątem ostrym więc nie ma wątpliwości ze znakiem pierwiastka). W zależności od znaku
jest kątem ostrym więc nie ma wątpliwości ze znakiem pierwiastka). W zależności od znaku 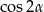 mamy więc
mamy więc
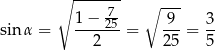
lub
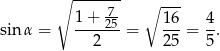
Odpowiedź: 0,6 i 0,8

