/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 4928240

Dodaj do ulubionych
Dodaj do rozwiązanych

W równoległoboku 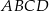ABCD miara kąta ostrego jest równa 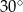∘ 30 , a odległości punktu przecięcia się przekątnych od sąsiednich boków równoległoboku są równe 2 i 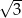√ -- 3 . Oblicz długość krótszej przekątnej tego równoległoboku.

Rozwiązanie

Zaczynamy oczywiście od rysunku.

PIC

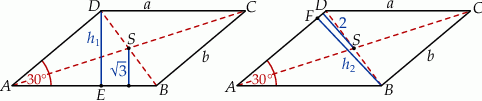
Ponieważ przekątne równoległoboku dzielą się na połowy, możemy łatwo obliczyć długości wysokości 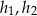h1,h2 równoległoboku.

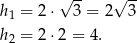
√ -- √ -- h1 = 2 ⋅ 3 = 2 3 h = 2 ⋅2 = 4. 2

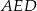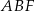Teraz z trójkątów prostokątnych AED i ABF możemy obliczyć długości boków równoległoboku.

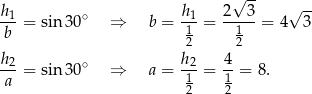
√ -- -- h1-= sin 30∘ ⇒ b = h1-= 2---3 = 4√ 3 b 1 1 2 2 h2-= sin 30∘ ⇒ a = h2-= 4- = 8. a 12 12

Obliczamy teraz długość krótszej przekątnej – korzystamy z twierdzenia cosinusów.

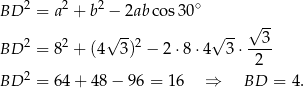
BD 2 = a2 + b 2 − 2ab cos 30∘ √ -- 2 2 √ --2 √ -- --3- BD = 8 + (4 3) − 2 ⋅8 ⋅4 3 ⋅ 2 2 BD = 64+ 48− 96 = 16 ⇒ BD = 4.

 
Odpowiedź: 4

Wersja PDF