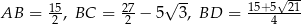Zadanie nr 7031570
W czworokąt 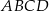 , w którym
, w którym 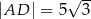 i
i 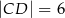 , można wpisać okrąg. Przekątna
, można wpisać okrąg. Przekątna 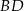 tworzy z bokiem
tworzy z bokiem 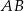 czworokąta kąt o mierze
czworokąta kąt o mierze 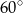 , natomiast z bokiem
, natomiast z bokiem 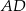 tworzy kąt, którego sinus jest równy
tworzy kąt, którego sinus jest równy  . Wyznacz długości boków
. Wyznacz długości boków 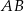 i
i 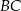 oraz długość przekątnej
oraz długość przekątnej 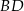 tego czworokąta.
tego czworokąta.
Rozwiązanie
Zaczynamy od szkicowego rysunku.
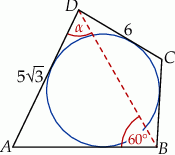
Długość boku 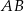 obliczamy pisząc twierdzenie sinusów w trójkącie
obliczamy pisząc twierdzenie sinusów w trójkącie 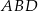 .
.
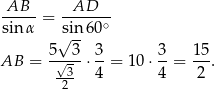
Teraz korzystamy z informacji o tym, że w czworokąt można wpisać okrąg – pozwoli to nam obliczyć długość boku 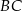 .
.
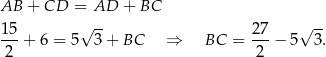
Długość przekątnej 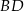 obliczymy pisząc twierdzenie cosinusów w trójkącie
obliczymy pisząc twierdzenie cosinusów w trójkącie 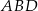 .
.
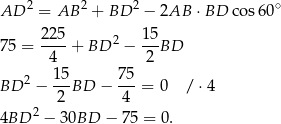
Rozwiązujemy otrzymane równanie kwadratowe.
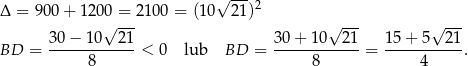
Ujemne rozwiązanie odrzucamy i mamy 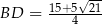 .
.
Odpowiedź: