/Szkoła średnia/Geometria/Planimetria/Czworokąt

Zadanie nr 7754595

Dodaj do ulubionych
Dodaj do rozwiązanych

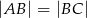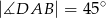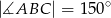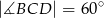Dany jest czworokąt wypukły ABCD , w którym: |AB | = |BC | , |∡DAB | = 45∘ , |∡ABC | = 150∘ , |∡BCD | = 60∘ . Wykaż, że trójkąt 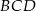BCD jest równoboczny.

Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

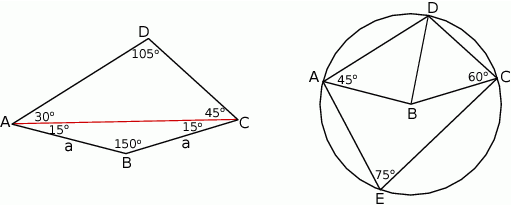
Sposób I

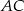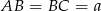Dorysujmy przekątną AC i oznaczmy AB = BC = a .

Pomysł jest następujący: spróbujemy pokazać, że 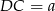DC = a , co będzie oznaczało, że trójkąt 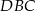DBC jest równoboczny. Odcinek 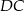DC obliczymy stosując twierdzenie sinusów w trójkącie 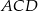ACD , ale zanim to zrobimy musimy obliczyć długość przekątnej AC .

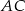Stosując twierdzenie cosinusów w trójkącie 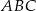ABC obliczamy długość odcinka AC .

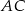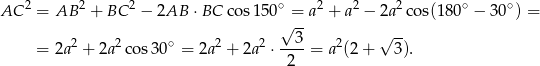
AC 2 = AB 2 + BC 2 − 2AB ⋅ BC cos 150∘ = a2 + a2 − 2a2 cos(180∘ − 30∘) = √ -- √ -- = 2a2 + 2a2cos 30∘ = 2a 2 + 2a 2 ⋅-3-= a2(2 + 3). 2

Teraz będziemy chcieli zastosować twierdzenie sinusów w trójkącie 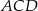ACD , ale zanim to zrobimy zauważmy, że

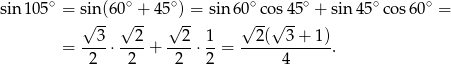
sin1 05∘ = sin(60∘ + 45∘) = sin 60∘ cos45 ∘ + sin 45∘co s60∘ = √ -- √ -- √ -- √ --√ -- --3- --2- --2- 1- --2(--3-+-1)- = 2 ⋅ 2 + 2 ⋅2 = 4 .

Stosujemy teraz twierdzenie sinusów w trójkącie 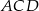ACD .

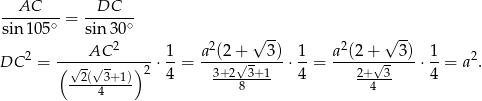
--AC---- = -DC---- sin 105∘ sin 30∘ √ -- √ -- AC 2 1 a2(2+ 3) 1 a2(2+ 3) 1 DC 2 = (-√--√----)-2 ⋅--= ----√------⋅ --= -----√-----⋅ --= a2. -2(-3+1)- 4 3+2-83+1 4 2+4-3 4 4

Zatem rzeczywiście 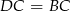DC = BC , co oznacza, że trójkąt 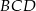BCD jest równoramienny z jednym z kątów równym 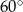∘ 60 , czyli jest równoboczny.

Sposób II

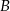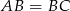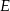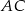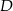Dorysujmy okrąg o środku B i promieniu AB = BC oraz niech E będzie dowolnym punktem tego okręgu leżącym po przeciwnej stronie prostej AC niż D . Mamy zatem

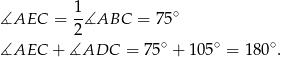
1 ∡AEC = -∡ABC = 75∘ 2 ∡AEC + ∡ADC = 7 5∘ + 105∘ = 180 ∘.

To oznacza, że punkt 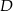D również leży na tym okręgu. W szczególności

DB = BC ,

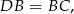
czyli trójkąt 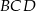BCD jest równoramienny z jednym z kątów równym 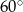60 ∘ . Jest więc równoboczny.

Wersja PDF