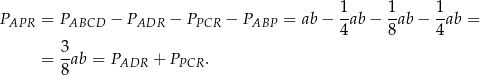Zadanie nr 8561900
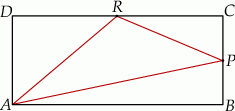
W prostokącie 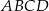 punkt
punkt 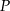 jest środkiem boku
jest środkiem boku 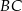 , a punkt
, a punkt 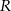 jest środkiem boku
jest środkiem boku 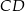 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 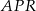 jest równe sumie pól trójkątów
jest równe sumie pól trójkątów 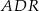 oraz
oraz 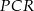 .
.
Rozwiązanie
Oznaczmy 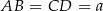 i
i 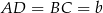 . Mamy zatem
. Mamy zatem
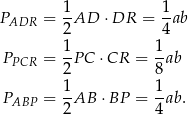
Stąd
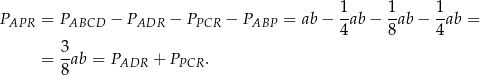
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
W prostokącie 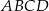 punkt
punkt  jest środkiem boku
jest środkiem boku 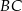 , a punkt
, a punkt 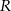 jest środkiem boku
jest środkiem boku 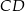 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 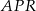 jest równe sumie pól trójkątów
jest równe sumie pól trójkątów 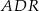 oraz
oraz 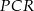 .
.

Oznaczmy 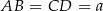 i
i 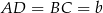 . Mamy zatem
. Mamy zatem
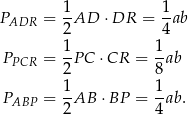
Stąd