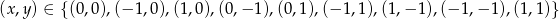Zadanie nr 2130001

Rozwiąż układ równań 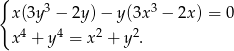{ 3 3 x(3y − 2y) − y(3x − 2x ) = 0 x4 + y4 = x2 + y2.

Rozwiązanie

Przekształćmy pierwsze równanie

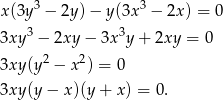
3 3 x(3y − 2y) − y(3x − 2x) = 0 3xy3 − 2xy − 3x 3y+ 2xy = 0 2 2 3xy(y − x ) = 0 3xy(y − x )(y+ x) = 0.

Mamy zatem cztery możliwości.
Jeżeli 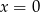x = 0 to drugie równanie przybiera postać

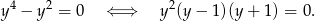
4 2 2 y − y = 0 ⇐ ⇒ y (y − 1)(y + 1 ) = 0.

Mamy zatem w tym przypadku trzy rozwiązania: 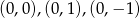(0,0),(0,1),(0,− 1) .
Jeżeli 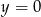y = 0 to drugie równanie ma postać

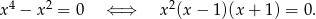
x 4 − x 2 = 0 ⇐ ⇒ x2(x − 1 )(x+ 1) = 0.

Mamy stąd dwa dodatkowe rozwiązania: 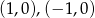(1 ,0 ),(−1 ,0) .
Jeżeli 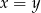x = y to drugie równanie ma postać

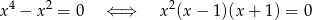
x4 − x2 = 0 ⇐ ⇒ x 2(x− 1)(x + 1) = 0

Otrzymujemy stąd dwa dodatkowe rozwiązania: 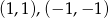(1,1),(− 1,− 1) .
Jeżeli wreszcie 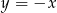y = −x to drugie równanie przybiera postać

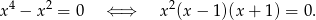
x 4 − x 2 = 0 ⇐ ⇒ x2(x − 1 )(x+ 1) = 0.

Otrzymujemy więc kolejne dwa rozwiązania: 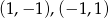(1,− 1),(− 1,1) .
W sumie jest więc 9 rozwiązań

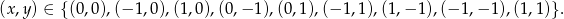
(x,y) ∈ {(0,0 ),(− 1 ,0 ),(1,0),(0,− 1),(0,1),(− 1,1),(1,− 1),(− 1&

Odpowiedź: (x ,y) ∈ {(0,0),(− 1,0),(1,0),(0,− 1),(0,1 ),(− 1 ,1 ),(1,− 1),(− 1