Zadanie nr 7176054
Prosta o równaniu 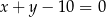 przecina okrąg o równaniu
przecina okrąg o równaniu 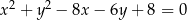 w punktach
w punktach 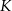 i
i 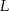 . Punkt
. Punkt 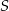 jest środkiem cięciwy
jest środkiem cięciwy 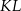 . Wyznacz równanie obrazu tego okręgu w jednokładności o środku
. Wyznacz równanie obrazu tego okręgu w jednokładności o środku 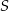 i skali
i skali 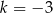 .
.
Rozwiązanie
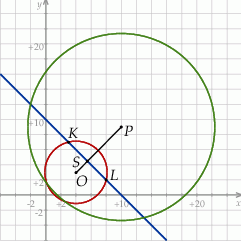
Przekształćmy równanie okręgu tak, żeby widzieć jaki jest jego środek i promień.
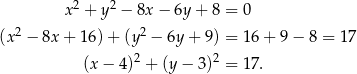
Jest to więc okrąg o środku 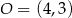 i promieniu
i promieniu 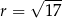 .
.
Znajdźmy teraz punkty wspólne tego okręgu z daną prostą – podstawiamy 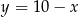 w równaniu okręgu.
w równaniu okręgu.
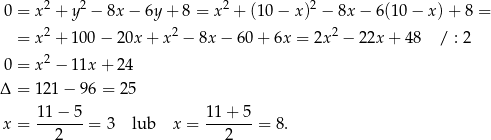
Stąd 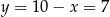 i
i 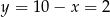 odpowiednio. Zatem
odpowiednio. Zatem 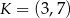 ,
, 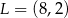 i
i
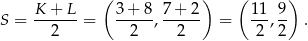
Obrazem danego okręgu w jednokładności o środku 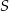 i skali
i skali 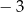 jest okrąg o promieniu
jest okrąg o promieniu 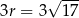 i środku
i środku 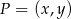 spełniającym warunek
spełniającym warunek
![−→ −→ SP = − 3SO [ 1 1 9 ] [ 11 9 ] [ 3 3] [ 9 9 ] x − ---,y − -- = − 3 4− --,3 − -- = − 3 − -,− -- = -,-- . 2 2 2 2 2 2 2 2](https://img.zadania.info/zad/7176054/HzadR15x.gif)
Stąd
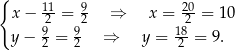
Zatem 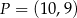 i szukany okrąg ma równanie
i szukany okrąg ma równanie
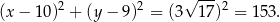
Odpowiedź: