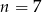/Szkoła średnia/Kombinatoryka/Symbol Newtona

Zadanie nr 5572506

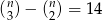Wyznacz liczbę n , wiedząc że n n (3)− (2) = 14 .

Wersja PDF

Rozwiązanie

Liczymy

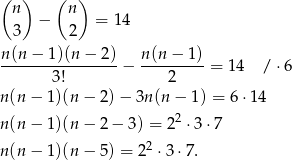
(n ) (n ) − = 14 3 2 n (n− 1)(n − 2) n (n− 1) ---------------- − --------- = 14 / ⋅6 3! 2 n(n − 1 )(n− 2)− 3n(n − 1) = 6 ⋅14 n(n − 1 )(n− 2− 3) = 22 ⋅ 3⋅7 n(n − 1 )(n− 5) = 22 ⋅ 3⋅7 .

Sposób I

Wypiszmy dzielniki 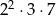22 ⋅ 3⋅7 :

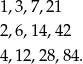
1,3,7 ,21 2,6,1 4,42 4,12 ,28,84.

Wszystkie liczby w rozkładzie powyżej są całkowite 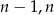n − 1,n są nieujemne, więc 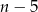n− 5 musi być dodatnie, czyli 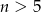n > 5 . Skoro 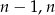n− 1,n różnią się o 1 to musi to być 6 i 7. Wtedy 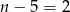n − 5 = 2 i wszystko się zgadza.

Sposób II

Zadanie możemy też rozwiązać ’na chama’, szukając pierwiastków wielomianu

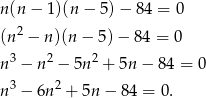
n(n − 1)(n − 5)− 8 4 = 0 2 (n − n)(n − 5) − 84 = 0 3 2 2 n − n − 5n + 5n − 8 4 = 0 n3 − 6n2 + 5n − 8 4 = 0.

Nie jest to zupełnie proste, bo jedyny pierwiastek tego wielomianu to 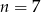n = 7 i aby go odnaleźć (sprawdzając dzielniki wyrazu wolnego) trzeba się trochę naliczyć. Ale jak już go mamy to dzielimy przez 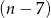(n− 7) . My zrobimy to grupując wyrazy.

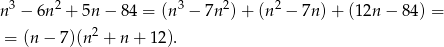
3 2 3 2 2 n − 6n + 5n − 84 = (n − 7n ) + (n − 7n) + (12n − 84) = = (n− 7)(n2 + n + 12).

Trójmian w nawiasie nie ma pierwiastków (ujemna 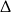Δ ), więc jedyne rozwiązanie to n = 7 .  
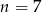Odpowiedź: n = 7

Wersja PDF
Rozwiązanie Losuj ponownie