Liczby  i
i 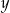 są dodatnie. Iloczyn potrojonej liczby
są dodatnie. Iloczyn potrojonej liczby  i liczby o 35% większej od liczby
i liczby o 35% większej od liczby 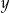 wyraża się wzorem
wyraża się wzorem
A) 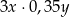 B)
B) 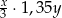 C)
C) 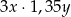 D)
D) 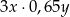
/Szkoła podstawowa/Zadania testowe/Procenty
Liczby  i
i 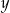 są dodatnie. Iloczyn potrojonej liczby
są dodatnie. Iloczyn potrojonej liczby  i liczby o 35% mniejszej od liczby
i liczby o 35% mniejszej od liczby 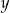 wyraża się wzorem
wyraża się wzorem
A) 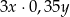 B)
B) 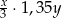 C)
C) 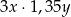 D)
D) 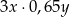
Liczby  i
i 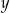 są dodatnie. Iloczyn trzeciej części liczby
są dodatnie. Iloczyn trzeciej części liczby  i liczby o 35% większej od liczby
i liczby o 35% większej od liczby 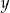 wyraża się wzorem
wyraża się wzorem
A) 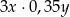 B)
B) 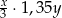 C)
C) 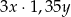 D)
D) 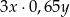
Piotrek ma w swojej bibliotece tylko książki historyczne i biograficzne. Książek historycznych ma 9, co stanowi 30% wszystkich jego książek. Wynika stąd, że liczba książek biograficznych Piotrka, to
A) 21 B) 30 C) 16 D) 10
Gienek ma w swojej bibliotece tylko książki przygodowe i historyczne. Książek historycznych ma 21, co stanowi 35% wszystkich jego książek. Wynika stąd, że liczba książek przygodowych Gienka, to
A) 21 B) 31 C) 39 D) 43
Karol ma w swojej bibliotece tylko książki przyrodnicze i sensacyjne. Książek przyrodniczych ma 12, co stanowi 40% wszystkich jego książek. Wynika stąd, że liczba książek sensacyjnych Karola, to
A) 21 B) 18 C) 36 D) 24
Gdy od 17% liczby 21 odejmiemy 21% liczby 17, to otrzymamy
A) 0 B) 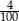 C) 3,57 D) 4
C) 3,57 D) 4
Gdy do 50% liczby 73 dodamy 73% liczby 50, to otrzymamy
A) 1 B) 73 C) 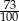 D) 100
D) 100
Gdy od 19% liczby 32 odejmiemy 16% liczby 19, to otrzymamy
A) 0 B) 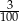 C) 3,04 D) 9,12
C) 3,04 D) 9,12
Do 200 ml soku dolano 0,3 litra wody. Stężenie soku w otrzymanym napoju jest równe
A) 66% B) 40% C) 150% D) 60%
Grupie dwustu osób zadano pytanie: „Jaka jest twoja ulubiona dyscyplina sportu?”. Wyniki tej ankiety przedstawiono na wykresie.
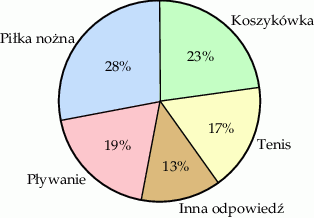
Z informacji podanych na diagramie wynika, że:
A) 28 osób jako ulubioną dyscyplinę podało piłkę nożną.
B) Łączna liczba odpowiedzi: „piłka nożna” i „tenis” jest równa liczbie wszystkich pozostałych odpowiedzi.
C) Liczba odpowiedzi „pływanie” była o 4 większa od liczby odpowiedzi „tenis”.
D) Liczba odpowiedzi „tenis” była o 6 mniejsza od liczby odpowiedzi „koszykówka”.
W pewnym banku oprocentowanie kredytu konsumpcyjnego przez cały marzec było równe 17%. Na początku kwietnia podwyższono oprocentowanie tego kredytu o 3 punkty procentowe, a na początku maja obniżono o 4 punkty procentowe. Oznacza to, że oprocentowanie tego kredytu konsumpcyjnego między kwietniem a majem zmalało o
A) 5% B) 3% C) 25% D) 20%
W pewnym sklepie ceny wszystkich płyt CD obniżono o 20%. Zatem za dwie płyty kupione w tym sklepie należy zapłacić mniej o
A) 10% B) 20% C) 30% D) 40%
Ile procent doby stanowi 15 minut?
A) około 1% B) 4% C) około 2% D) 12,5%
Karolina ma o 25% wyższy wynik z egzaminu próbnego od Oli. Wynika z tego, że Oli wynik jest niższy od wyniku Karoliny o
A) 25% B) 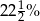 C) 20% D)
C) 20% D) 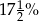
W klasie Ia jest o 25% więcej uczniów niż w klasie Ib. Stąd wynika, że w klasie Ib jest mniej uczniów niż w klasie Ia o
A) 25% B) 75% C) 20% D) 50%
Połowę liczby  zwiększono o 20%. Otrzymano
zwiększono o 20%. Otrzymano
A) 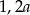 B)
B) 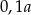 C)
C) 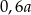 D)
D) 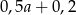
Połowę liczby  zwiększono o 40%. Otrzymano
zwiększono o 40%. Otrzymano
A) 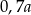 B)
B) 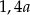 C)
C) 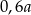 D)
D) 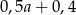
Jedną trzecią dodatniej liczby  zwiększono o 20%. Otrzymano w ten sposób
zwiększono o 20%. Otrzymano w ten sposób
A) 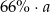 B)
B) 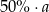 C)
C) 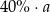 D)
D) 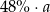
Ćwierć liczby  zwiększono o 40%. Otrzymano
zwiększono o 40%. Otrzymano
A) 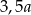 B)
B) 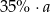 C)
C) 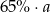 D)
D) 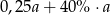
Połowę liczby  zmniejszono o 20%. Otrzymano
zmniejszono o 20%. Otrzymano
A) 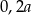 B)
B) 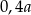 C)
C) 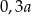 D)
D) 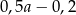
Jeżeli liczba 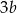 jest o 20% większa od połowy liczby
jest o 20% większa od połowy liczby 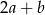 , to liczba
, to liczba  jest większa od
jest większa od 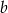 o
o
A) 100% B) 80% C) 50% D) 200%
Połowa liczby  jest o 25% mniejsza od trzeciej części liczby
jest o 25% mniejsza od trzeciej części liczby 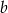 . Wtedy liczba
. Wtedy liczba 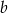 jest
jest
A) o 200% większa od 
B) o 100% większa od 
C) o 50% większa od 
D) o 150% większa od 
Jeżeli liczba 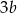 jest o 50% większa od połowy liczby
jest o 50% większa od połowy liczby 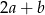 , to liczba
, to liczba  jest większa od
jest większa od 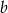 o
o
A) 100% B) 150% C) 50% D) 200%
Na rysunku przedstawiono skład jednego ze stopów miedzi, mosiądzu, który jest wykorzystywany głównie do odlewania przedmiotów ozdobnych. Ile potrzeba cynku do odlania 2000 kg ozdób?

A) 1600 kg B) 400 kg C) 600 kg D) 750 kg
Na rysunku przedstawiono skład jednego ze stopów miedzi, brązu, który jest wykorzystywany między innymi do odlewania dzwonów. Ile potrzeba miedzi do odlania dzwonu ważącego 10000 kg?

A) 76 kg B) 2400 kg C) 4800 kg D) 7600 kg
Na rysunku przedstawiono skład jednego ze stopów miedzi, zwanego „złotem mainnheimskim”, który jest wykorzystywany do wyrobu sztucznej biżuterii. Ile potrzeba cynku do wykonania 1500 kg biżuterii?

A) 135 kg B) 1200 kg C) 600 kg D) 165 kg
Liczba osobników pewnego zagrożonego wyginięciem gatunku zwierząt wzrosła w stosunku do liczby tych zwierząt z 31 grudnia 2011 r. o 120% i obecnie jest równa 8910. Ile zwierząt liczyła populacja tego gatunku w ostatnim dniu 2011 roku?
A) 4050 B) 1782 C) 7425 D) 7128
Cena jednego bitcoina wzrosła w stosunku do ceny jednego bitcoina z dnia 1 stycznia 2017 o 1000% i wynosiła w grudniu 2017 roku 46860 zł. Jaka była cena jednego bitcoina w pierwszym dniu 2017 roku?
A) 4686 zł B) 527 zł C) 4260 zł D) 468 zł
Liczba uczniów pewnej szkoły zmalała w stosunku do 1 września 2010 roku o 25% i obecenie jest równa 735. Ilu uczniów liczyła ta szkoła na początku roku szkolnego 2010/2011?
A) 551 B) 919 C) 980 D) 1050
Oprocentowanie kredytu konsumpcyjnego wynosiło w marcu 16%. W kwietniu wzrosło o 25%. O ile punktów procentowych zwiększyło się oprocentowanie kredytu?
A) o 4 B) o 9 C) o 25 D) o 41
Oprocentowanie kredytu konsumpcyjnego wynosiło w marcu 20%. W kwietniu wzrosło o 20%. O ile punktów procentowych zwiększyło się oprocentowanie kredytu?
A) o 0 B) o 20 C) o 4 D) o 40
Oprocentowanie kredytu konsumpcyjnego wynosiło w marcu 15%. W kwietniu wzrosło o 30%. O ile punktów procentowych zwiększyło się oprocentowanie kredytu?
A) o 45 B) o 30 C) o 15 D) o 4,5
W klasie jest o 25% więcej chłopców niż dziewcząt. Jaką część wszystkich uczniów tej klasy stanowią chłopcy?
A) 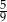 B)
B) 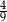 C)
C) 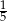 D)
D) 
W klasie jest o 15% więcej chłopców niż dziewcząt. Jaką część wszystkich uczniów tej klasy stanowią chłopcy?
A) 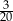 B)
B) 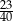 C)
C) 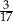 D)
D) 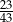
Dziewczęta stanowią 30% uczniów w pewnej klasy. Wynika stąd, że chłopcy stanowią
A) 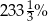 liczby dziewcząt B)
liczby dziewcząt B) 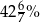 liczby dziewcząt
liczby dziewcząt
C) 21% liczby dziewcząt D) 70% liczby dziewcząt
Dziewczęta stanowią 40% uczniów w pewnej klasy. Wynika stąd, że chłopcy stanowią
A) 50% liczby dziewcząt B) 150% liczby dziewcząt
C) 60% liczby dziewcząt D) 120% liczby dziewcząt
Chłopcy stanowią 25% uczniów w pewnej klasy. Wynika stąd, że dziewczęta stanowią
A) 175% liczby chłopców B) 200% liczby chłopców
C) 75% liczby chłopców D) 300% liczby chłopców
Dana jest liczba 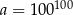 . Liczba
. Liczba 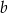 stanowi 1% liczby
stanowi 1% liczby  . Wówczas
. Wówczas
A) 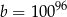 B)
B) 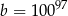 C)
C) 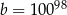 D)
D) 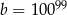
Płyta kosztowała 80 zł, a po obniżce 60 zł. O ile procent obniżono cenę płyty?
A) 20% B) 25% C) 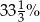 D) 75%
D) 75%
Narty kosztowały 680 zł. O ile procent należałoby obniżyć cenę nart, aby kosztowały 595 zł?
A) 8,5% B) 12,5% C) 14,2% D) 25%
Odtwarzacz kosztujący 340 zł sprzedano podczas wyprzedaży za 255 zł. Obniżka wynosiła
A) 15% B) 20% C) 40% D) 25%
Buty, które kosztowały 220 złotych, przeceniono i sprzedano za 176 złotych. O ile procent obniżono cenę butów?
A) 80 B) 20 C) 22 D) 44
W ramach wyprzedaży sezonowej płaszcz o początkowej wartości 240 zł przeceniono na 200 zł. Zatem cenę tego płaszcza obniżono o
A) 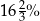 jego początkowej wartości.
jego początkowej wartości.
B) 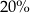 jego początkowej wartości.
jego początkowej wartości.
C) 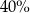 jego początkowej wartości.
jego początkowej wartości.
D) 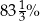 jego początkowej wartości.
jego początkowej wartości.
Rower kosztujący 270 zł sprzedano podczas wyprzedaży za 216 zł. Obniżka wynosiła
A) 15% B) 20% C) 40% D) 80%
Książka kosztowała 75 zł, a po obniżce 60 zł. O ile procent obniżono cenę książki?
A) 20% B) 25% C) 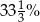 D) 75%
D) 75%
Kurtkę, która kosztowała 450 złotych, przeceniono i sprzedano za 387 złotych. O ile procent obniżono cenę kurtki?
A) 14 B) 15 C) 20 D) 24
Suma liczby  i
i 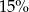 tej liczby jest równa 230. Równaniem opisującym tę zależność jest
tej liczby jest równa 230. Równaniem opisującym tę zależność jest
A) 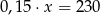 B)
B) 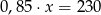 C)
C) 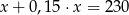 D)
D) 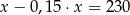
Różnica liczby  i
i 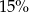 tej liczby jest równa 255. Równaniem opisującym tę zależność jest
tej liczby jest równa 255. Równaniem opisującym tę zależność jest
A) 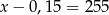 B)
B) 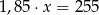 C)
C) 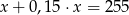 D)
D) 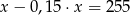
Firma składa się z dwóch oddziałów. W marcu zysk pierwszego oddziału był równy 30 tys. zł, a drugiego oddziału 24 tys. zł. W kwietniu zysk pierwszego oddziału zmniejszył się o 10% w stosunku do marca, ale zysk całej firmy był taki sam jak w marcu.
O ile procent w stosunku do poprzedniego miesiąca zwiększył się w kwietniu zysk drugiego oddziału?
A) 10% B) 12,5% C) 8% D) 14,5%

