/Szkoła średnia/Zadania maturalne/Matura 2015
Egzamin Maturalny
z Matematyki (termin dodatkowy)
poziom rozszerzony 2 czerwca 2015 Czas pracy: 180 minut
Zadania zamknięte
Ciąg 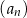 jest określony wzorem
jest określony wzorem 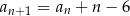 dla każdej liczby naturalnej
dla każdej liczby naturalnej 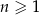 . Trzeci wyraz tego ciągu jest równy
. Trzeci wyraz tego ciągu jest równy 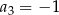 . Wyraz
. Wyraz 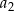 jest równy
jest równy
A) 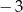 B)
B) 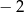 C) 2 D) 3
C) 2 D) 3
Liczba punktów wspólnych wykresów funkcji 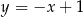 i
i 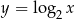 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Która z poniższych funkcji, określonych w zbiorze liczb rzeczywistych, nie ma minimum lokalnego ani maksimum lokalnego?
A) 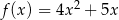 B)
B) 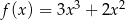 C)
C) 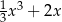 D)
D) 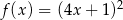
Dla dowolnego kąta  wartość wyrażenia
wartość wyrażenia 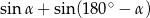 jest równa wartości wyrażenia
jest równa wartości wyrażenia
A) 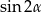 B)
B) 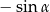 C)
C) 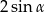 D) 0
D) 0
Zbiór 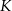 – to zbiór wszystkich liczb rzeczywistych
– to zbiór wszystkich liczb rzeczywistych  , dla których wartość liczbowa wyrażenia
, dla których wartość liczbowa wyrażenia 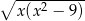 jest liczbą rzeczywistą. Zatem
jest liczbą rzeczywistą. Zatem
A) 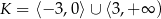 B)
B) 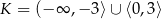
C) 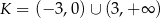 D)
D) 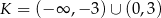
Zadania otwarte
Wyznacz największą liczbę całkowitą spełniającą nierówność 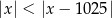 .
.
Prosta o równaniu 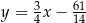 jest styczna od okręgu o środku
jest styczna od okręgu o środku 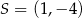 . Wyznacz promień tego okręgu.
. Wyznacz promień tego okręgu.
Niech 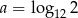 . Wykaż, że
. Wykaż, że 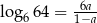 .
.
W trójkącie 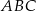 kąt wewnętrzny przy wierzchołku
kąt wewnętrzny przy wierzchołku 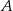 ma miarę
ma miarę 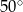 , a kąt wewnętrzny przy wierzchołku
, a kąt wewnętrzny przy wierzchołku 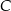 ma miarę
ma miarę 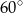 . Okrąg
. Okrąg 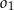 przechodzi przez punkt
przechodzi przez punkt 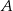 i przecina boki
i przecina boki 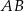 i
i 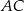 trójkąta odpowiednio w punktach
trójkąta odpowiednio w punktach 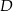 i
i 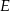 . Okrąg
. Okrąg 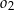 przechodzi przez punkt
przechodzi przez punkt 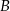 , przecina okrąg
, przecina okrąg 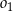 w punkcie
w punkcie 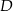 oraz w punkcie
oraz w punkcie 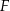 leżącym wewnątrz trójkąta
leżącym wewnątrz trójkąta 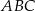 . Ponadto okrąg
. Ponadto okrąg 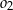 przecina bok
przecina bok 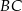 trójkąta w punkcie
trójkąta w punkcie 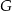 .
.
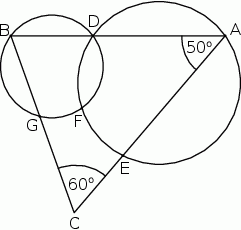
Udowodnij, że na czworokącie 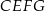 można opisać okrąg.
można opisać okrąg.
Rozwiąż równanie 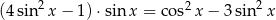 , dla
, dla 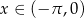 .
.
W trójkąt prostokątny o przyprostokątnych długości 15 i 20 wpisano okrąg. Oblicz długość odcinka łączącego wierzchołek kąta prostego tego trójkąta z punktem wspólnym okręgu i przeciwprostokątnej.
Dany jest trójkąt 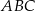 , w którym
, w którym 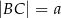 . Z wierzchołka
. Z wierzchołka 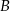 poprowadzono środkową
poprowadzono środkową 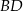 do boku
do boku 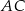 . Punkt
. Punkt 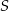 jest środkiem odcinka
jest środkiem odcinka 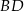 . Przez punkty
. Przez punkty 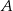 i
i 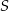 poprowadzono prostą, która przecięła bok
poprowadzono prostą, która przecięła bok 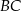 w punkcie
w punkcie 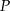 . Wykaż, że długość odcinka
. Wykaż, że długość odcinka 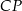 jest równa
jest równa 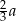 .
.
Oblicz, ile jest wszystkich liczb naturalnych pięciocyfrowych parzystych, w których zapisie występują co najwyżej dwie dwójki.
Podstawą ostrosłupa 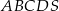 jest trapez
jest trapez 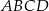 . Przekątna
. Przekątna 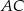 tego trapezu ma długość
tego trapezu ma długość 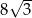 , jest prostopadła do ramienia
, jest prostopadła do ramienia 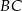 i tworzy z dłuższą podstawą
i tworzy z dłuższą podstawą 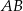 tego trapezu kąt o mierze
tego trapezu kąt o mierze 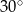 . Każda krawędź boczna tego ostrosłupa ma tę samą długość
. Każda krawędź boczna tego ostrosłupa ma tę samą długość 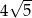 . Oblicz odległość spodka wysokości tego ostrosłupa od jego krawędzi bocznej
. Oblicz odległość spodka wysokości tego ostrosłupa od jego krawędzi bocznej 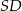 .
.
Funkcja 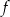 jest określona wzorem
jest określona wzorem 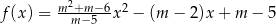 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz całkowite wartości parametru
. Wyznacz całkowite wartości parametru 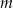 , dla których funkcja
, dla których funkcja 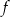 przyjmuje wartość największą i ma dwa różne miejsca zerowe o jednakowych znakach.
przyjmuje wartość największą i ma dwa różne miejsca zerowe o jednakowych znakach.
Rozpatrujemy wszystkie stożki, w których suma długości tworzącej i promienia podstawy jest równa 2. Wyznacz wysokość tego spośród rozpatrywanych stożków, którego objętość jest największa. Oblicz tę objętość.

