Zadania.info
Największy internetowy zbiór zadań z matematyki
cornersUpL
cornersUpR

Zadania

Na skróty

Recenzje

Linki sponsorowane

cornersM
Zaloguj się

Linki sponsorowane

cornersR
Zadanie nr 8761743

Odcinek 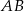AB o długości 4 jest zawarty w prostej o równaniu 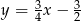3 3 y = 4x − 2 . Symetralna odcinka 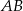AB przecina oś 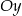Oy w punkcie 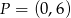P = (0,6) . Oblicz współrzędne końców odcinka AB .

Wersja PDF
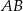Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

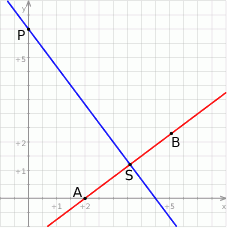
Rozpocznijmy od napisania symetralnej odcinka 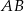AB – mając jej równanie łatwo wyznaczymy środek 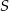S odcinka 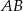AB . Prosta 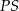P S jest prostopadła do prostej 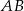AB , więc ma równanie postaci 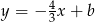y = − 4x + b 3 . Współczynnik 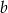b wyznaczamy podstawiając współrzędne punktu P .

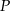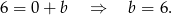
6 = 0+ b ⇒ b = 6.

Szukamy teraz punktu wspólnego S symetralnej 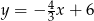4 y = − 3x + 6 odcinka AB i prostej AB .

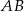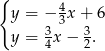
{ 4 y = − 3x + 6 y = 34x − 32 .

Odejmujemy od drugiego równania pierwsze (żeby skrócić 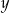y ) i mamy

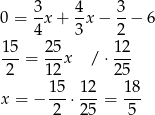
3- 4- 3- 0 = 4x + 3x − 2 − 6 15 25 12 ---= --x /⋅ --- 2 12 25 15- 12- 18- x = − 2 ⋅25 = 5

Stąd

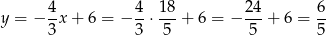
4 4 18 24 6 y = − --x+ 6 = − --⋅---+ 6 = − ---+ 6 = -- 3 3 5 5 5

i 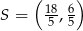( ) S = 18, 6 5 5 . Szukamy teraz punktów 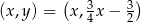(x ,y) = (x, 3 x− 3) 4 2 prostej 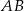AB , które są odległe od 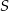S o 2.

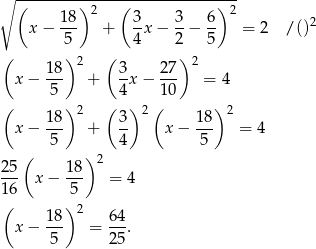
∘ (-------)-----(------------)--- 18 2 3 3 6 2 2 x − --- + -x − --− -- = 2 / () ( 5) ( 4 2) 5 18 2 3 27 2 x − --- + -x − --- = 4 ( 5 ) ( 4) (10 ) 18 2 3 2 18 2 x − --- + -- x − --- = 4 ( 5 ) 4 5 2 5 1 8 2 --- x − --- = 4 1(6 )5 18 2 64 x − 5-- = 25-.

Mamy stąd

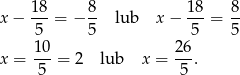
18 8 18 8 x − ---= − -- lub x − ---= -- 5 5 5 5 x = 10-= 2 lub x = 26. 5 5

Obliczamy jeszcze odpowiadające tym wartościom 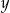y –ki.

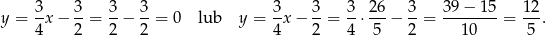
3 3 3 3 3 3 3 26 3 39 − 15 12 y = --x− --= -− --= 0 lub y = -x − --= --⋅---− --= --------= ---. 4 2 2 2 4 2 4 5 2 10 5

 
Odpowiedź: 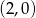(2,0) i ( ) 26, 12 5 5

Wersja PDF
Twoje uwagi
Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!