Zadanie nr 5894258
Ile jest wszystkich liczb naturalnych dwucyfrowych podzielnych przez 6 i niepodzielnych przez 9?
A) 6 B) 10 C) 12 D) 15
Rozwiązanie
Sposób I
Dwucyfrowe liczby podzielne przez 6 to
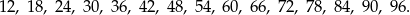
Wśród tych liczb jest 5 liczb podzielnych przez 9:
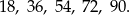
W sumie jest więc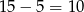 
takich liczb.
Sposób II
Dwucyfrowe liczby podzielne przez 6 to
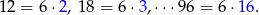
Jest ich więc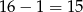 
. Liczby podzielne przez 6 i 9 to liczby podzielne przez 18, czyli liczby:
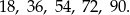
W sumie jest więc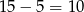 
takich liczb.
Odpowiedź: B
