Zadania.info Największy internetowy zbiór zadań z matematyki

/Szkoła średnia/Geometria/Geometria analityczna/Zadania na ekstremum/Inne

Wyszukiwanie zadań

Znajdź taki punkt 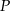P leżący na prostej 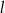l o równaniu 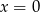x = 0 , z którego odcinek 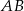AB , gdzie 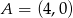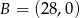A = (4,0) , B = (28,0) , widać pod możliwie największym kątem. Wyznacz ten kąt.

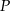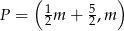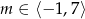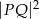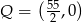W układzie współrzędnych rozważmy wszystkie punkty P postaci: ( ) P = 1m + 5,m 2 2 , gdzie m ∈ ⟨− 1,7⟩ . Oblicz najmniejszą i największą wartość 2 |PQ | , gdzie ( 55 ) Q = 2-,0 .

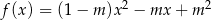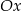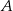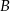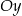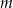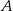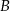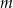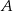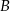Wykres funkcji kwadratowej 2 2 f(x) = (1 − m )x − mx + m przecina oś Ox w punktach A i B , które leżą po dwóch różnych stronach osi Oy . Wyznacz tę wartość parametru m , dla której iloczyn odległości punktów A i B od początku układu współrzędnych jest najmniejszy możliwy. Dla wyznaczonej wartości m oblicz sumę odległości punktów A i B od początku układu współrzędnych.