/Szkoła średnia/Ciągi

Zadanie nr 1970028

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyrazy ciągu geometrycznego 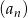(an) , określonego dla 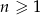n ≥ 1 , spełniają układ równań

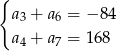
{ a3 + a6 = − 84 a + a = 168 4 7

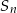Wyznacz liczbę n początkowych wyrazów tego ciągu, których suma Sn jest równa 32769.

Rozwiązanie

Jeżeli oznaczymy przez 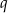q iloraz ciągu 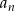an , to

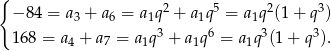
{ 2 5 2 3 − 84 = a3 + a6 = a 1q + a1q = a1q (1+ q ) 168 = a4 + a 7 = a1q3 + a1q6 = a1q3(1 + q3).

Dzielimy drugie równanie przez pierwsze i mamy

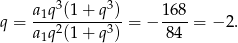
a1q3(1 + q3) 168 q = ---2------3--= − ----= − 2. a1q (1 + q ) 8 4

Z pierwszego równania mamy więc

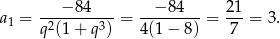
− 84 − 84 21 a1 = -2------3--= ---------= ---= 3 . q (1 + q ) 4(1 − 8) 7

Pozostało teraz rozwiązać równanie

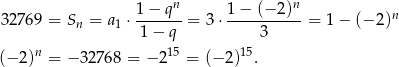
n n 3276 9 = Sn = a 1 ⋅ 1-−-q-= 3⋅ 1−--(−-2)--= 1 − (− 2)n 1− q 3 (−2 )n = − 32768 = − 215 = (− 2)15.

Stąd 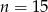n = 1 5 .  
Odpowiedź: n = 15

Wersja PDF