Zadanie nr 3571853
Ciąg 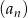 jest arytmetyczny oraz
jest arytmetyczny oraz 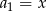 i
i 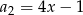 . Wiedząc, że
. Wiedząc, że 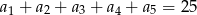 oblicz
oblicz  oraz sumę
oraz sumę 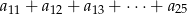 .
.
Rozwiązanie
Różnica danego ciągu jest równa
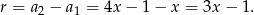
Zatem
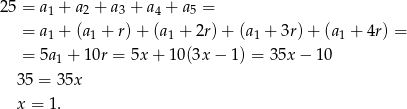
Stąd 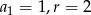 i ze wzoru na sumę
i ze wzoru na sumę 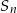 początkowych wyrazów ciągu arytmetycznego mamy
początkowych wyrazów ciągu arytmetycznego mamy
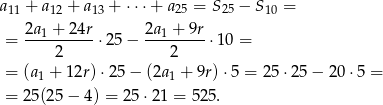
Odpowiedź: 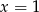 , suma: 525
, suma: 525
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Ciąg 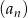 jest arytmetyczny oraz
jest arytmetyczny oraz 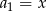 i
i 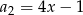 . Wiedząc, że
. Wiedząc, że 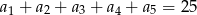 oblicz
oblicz  oraz sumę
oraz sumę 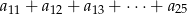 .
.
Różnica danego ciągu jest równa
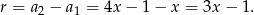
Zatem
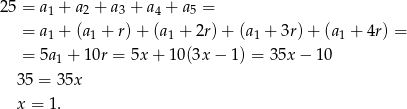
Stąd 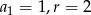 i ze wzoru na sumę
i ze wzoru na sumę 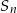 początkowych wyrazów ciągu arytmetycznego mamy
początkowych wyrazów ciągu arytmetycznego mamy
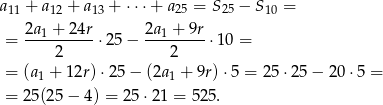
Odpowiedź: 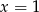 , suma: 525
, suma: 525
