Zadanie nr 4286658
Dany jest rosnący ciąg geometryczny 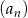 dla
dla 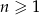 , w którym
, w którym 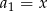 ,
, 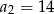 ,
, 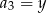 . Oblicz
. Oblicz  oraz
oraz 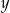 , jeżeli wiadomo, że
, jeżeli wiadomo, że 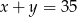 .
.
Rozwiązanie
Jedną z podstawowych własności ciągu geometrycznego jest fakt
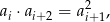
czyli kwadrat dowolnego wyrazu jest iloczynem wyrazów sąsiednich (wynika to łatwo z definicji ciągu geometrycznego). W naszej sytuacji oznacza to, że 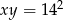 . Dostajemy zatem układ równań
. Dostajemy zatem układ równań
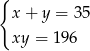
Wyliczając z pierwszego równania 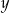 i wstawiając do drugiego, otrzymujemy
i wstawiając do drugiego, otrzymujemy
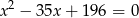
Równanie to ma dwa rozwiązania 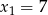 i
i 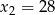 , co daje odpowiednio
, co daje odpowiednio 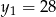 i
i 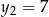 . Tylko para
. Tylko para 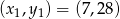 daje rosnący ciąg geometryczny.
daje rosnący ciąg geometryczny.
Odpowiedź: