Zadanie nr 4435659
Długości boków trójkąta 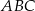 są kolejnymi wyrazami ciągu arytmetycznego, a jeden z jego kątów ma miarę
są kolejnymi wyrazami ciągu arytmetycznego, a jeden z jego kątów ma miarę 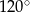 . Objętość prostopadłościanu, którego trzy krawędzie mają taką samą długość jak boki trójkąta
. Objętość prostopadłościanu, którego trzy krawędzie mają taką samą długość jak boki trójkąta 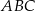 jest równa 840. Oblicz objętość największej kuli jaka może być umieszczona wewnątrz tego prostopadłościanu.
jest równa 840. Oblicz objętość największej kuli jaka może być umieszczona wewnątrz tego prostopadłościanu.
Rozwiązanie
Zacznijmy od szkicowego rysunku i oznaczmy boki trójkąta przez 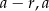 i
i 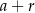 , gdzie
, gdzie 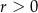 .
.
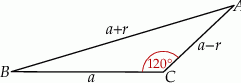
Ponieważ w trójkącie naprzeciw większego kąta leży większy bok, kąt o mierze 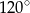 leży naprzeciwko boku długości
leży naprzeciwko boku długości 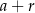 . Piszemy twierdzenie cosinusów w tym trójkącie
. Piszemy twierdzenie cosinusów w tym trójkącie
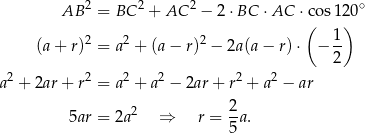
Stąd
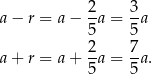
Boki trójkąta 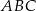 mają więc długości:
mają więc długości: 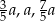 . Łatwo teraz wykorzystać podaną informację o objętości prostopadłościanu:
. Łatwo teraz wykorzystać podaną informację o objętości prostopadłościanu:
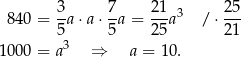
Szkicujemy prostopadłościan – musimy ustalić jaką największą kulę możemy w nim umieścić.
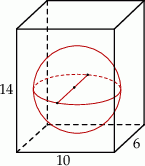
Zauważmy, że każda kula zawarta w prostopadłościanie ma średnicę mniejszą niż każda z krawędzi prostopadłościanu. W takim razie średnica kuli umieszczonej w prostopadłościanie opisanym w treści zadania nie może być większa niż 6. Z drugiej strony, kula o średnicy 6 mieści się w całości w prostopadłościanie, więc interesująca nas objętość jest równa
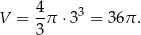
Odpowiedź: