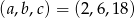Zadanie nr 6771462
Ciąg 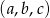 jest geometryczny i
jest geometryczny i 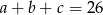 , zaś ciąg
, zaś ciąg 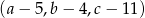 jest arytmetyczny. Oblicz
jest arytmetyczny. Oblicz 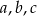 .
.
Rozwiązanie
Sposób I
Skoro liczby 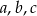 tworzą ciąg geometryczny to są postaci
tworzą ciąg geometryczny to są postaci 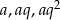 . Z podanej sumy mamy
. Z podanej sumy mamy
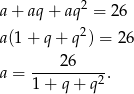
Z informacji o ciągu arytmetycznym wiemy, że liczby
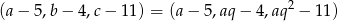
są kolejnymi wyrazami ciągu arytmetycznego. Mamy zatem
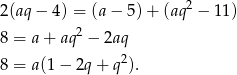
Podstawiamy teraz 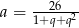 .
.
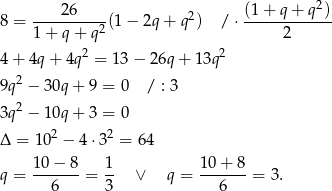
Dla 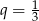 mamy
mamy
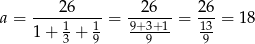
i wtedy 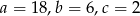 .
.
Dla 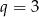 mamy
mamy
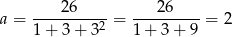
i wtedy 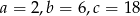 .
.
Sposób II
Liczby 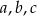 są kolejnymi wyrazami ciągu geometrycznego, czyli
są kolejnymi wyrazami ciągu geometrycznego, czyli 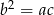 . Wiemy ponadto, że
. Wiemy ponadto, że
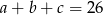
oraz liczby 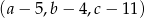 są kolejnymi wyrazami ciągu arytmetycznego, czyli
są kolejnymi wyrazami ciągu arytmetycznego, czyli
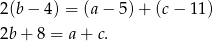
Podstawiając 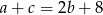 w równości
w równości 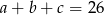 mamy
mamy

Zatem
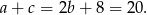
Podstawiamy teraz 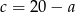 do równości
do równości 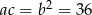 .
.
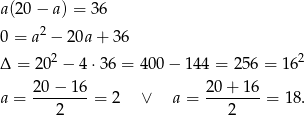
Mamy wtedy odpowiednio 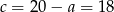 i
i 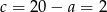 odpowiednio.
odpowiednio.
Odpowiedź: 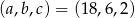 lub
lub