Zadanie nr 6963821
Dany jest ciąg arytmetyczny 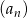 , gdzie
, gdzie 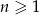 . Wiadomo, że dla każdego
. Wiadomo, że dla każdego 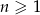 suma
suma  początkowych wyrazów
początkowych wyrazów 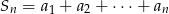 wyraża się wzorem:
wyraża się wzorem: 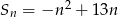 .
.
- Wyznacz wzór na
 –ty wyraz ciągu
–ty wyraz ciągu 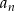 .
. - Oblicz
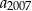 .
. - Wyznacz liczbę
 , dla której
, dla której 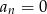 . .
. .
Rozwiązanie
- Ponieważ
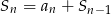 , to
, to 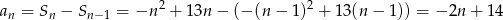
Odpowiedź: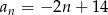
- Korzystając z powyższego wzoru:
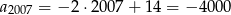
Odpowiedź: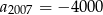
- Ponownie korzystamy z wyprowadzonego wzoru:
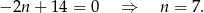
Odpowiedź: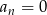 dla
dla 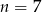 .
.

