/Szkoła średnia/Zadania maturalne/Matura 2016/Matura próbna/CKE, OKE, CEN
Lubelska próba przed maturą
z matematyki poziom rozszerzony 9 marca 2016 Czas pracy: 180 minut
Zadania zamknięte
Wiadomo, że 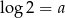 oraz
oraz 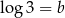 . Zatem
. Zatem 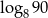 jest równy
jest równy
A) 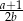 B)
B) 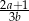 C)
C) 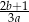 D)
D) 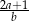
Ile jest liczb całkowitych spełniających nierówność 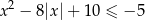 ?
?
A) 1 B) 2 C) 3 D) 6
Zbiorem wartości funkcji 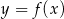 jest przedział
jest przedział 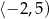 . Zatem zbiorem wartości funkcji
. Zatem zbiorem wartości funkcji 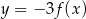 jest przedział
jest przedział
A) 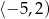 B)
B) 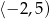 C)
C) 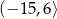 D)
D) 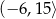
W turnieju szachowym rozegrano 36 partii. Każdy zawodnik rozegrał z każdy dokładnie 1 mecz. Ilu zawodników brało udział w turnieju?
A) 10 B) 9 C) 8 D) 7
Granica jednostronna 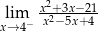 jest równa
jest równa
A) 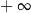 B)
B) 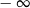 C)
C) 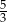 D)
D) 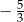
Zadania otwarte
Dla jakiej wartości parametru 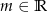 funkcja
funkcja 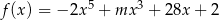 ma ekstremum w punkcie
ma ekstremum w punkcie 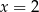 ?
?
W czworokącie wypukłym 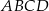 poprowadzono przekątną
poprowadzono przekątną 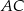 . Okręgi wpisane w trójkąty
. Okręgi wpisane w trójkąty 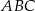 i
i 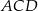 są styczne zewnętrznie. Wykaż, że w czworokąt
są styczne zewnętrznie. Wykaż, że w czworokąt 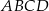 można wpisać okrąg.
można wpisać okrąg.
Określ dziedzinę i zbiór wartości funkcji 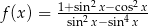 .
.
Dla jakich wartości parametru 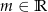 pierwiastek równania
pierwiastek równania 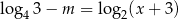 należy do przedziału
należy do przedziału 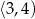 ?
?
Znajdź równanie stycznej do wykresu funkcji 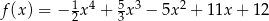 , która jest równoległa do prostej o równaniu
, która jest równoległa do prostej o równaniu 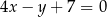 .
.
Sprawdź dla jakiego 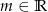 pierwiastki wielomianu
pierwiastki wielomianu 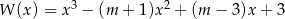 tworzą ciąg arytmetyczny?
tworzą ciąg arytmetyczny?
Suma nieskończonego zbieżnego ciągu geometrycznego jest równa 56, a suma kwadratów wyrazów tego ciągu jest równa 448. Znajdź pierwszy wyraz tego ciągu i napisz wzór na wyraz ogólny.
Udowodnij, że dla każdej liczby rzeczywistej  i każdej liczby rzeczywistej
i każdej liczby rzeczywistej 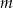 prawdziwa jest nierówność
prawdziwa jest nierówność 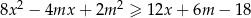 .
.
W prostokątnym układzie współrzędnych narysuj zbiór tych wszystkich punktów o współrzędnych 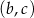 , dla których różne pierwiastki
, dla których różne pierwiastki 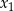 i
i 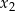 równania
równania 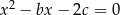 spełniają warunek
spełniają warunek 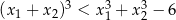 .
.
Podstawą prostopadłościanu jest prostokąt o stosunku boków 1:3. Objętość bryły jest równa 12. Oblicz wymiary tego prostopadłościanu, aby jego powierzchnia całkowita była najmniejsza. Oblicz tę najmniejszą powierzchnię.
Doświadczenie losowe polega na tym, że losujemy jednocześnie trzy liczby ze zbioru
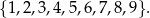
Oblicz prawdopodobieństwo warunkowe, że wśród wylosowanych liczb będzie liczba 3, pod warunkiem, że suma wylosowanych liczb będzie nieparzysta. Wynik przedstaw w postaci ułamka nieskracalnego.
Okrąg 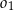 o równaniu
o równaniu 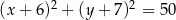 oraz okrąg
oraz okrąg 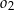 o środku
o środku 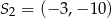 są wewnętrznie styczne, przy czym okrąg
są wewnętrznie styczne, przy czym okrąg 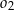 zawiera się w kole opisanym nierównością
zawiera się w kole opisanym nierównością 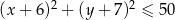 . Napisz równanie wspólnej stycznej do obu okręgów.
. Napisz równanie wspólnej stycznej do obu okręgów.

