Zadanie nr 6950778
Nieskończony ciąg liczbowy jest określony wzorem 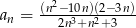 dla
dla 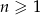 . Wtedy
. Wtedy
A) 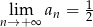 B)
B) 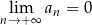 C)
C) 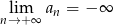 D)
D) 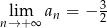
Rozwiązanie
Liczymy (dzielimy licznik i mianownik przez 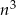 ).
).
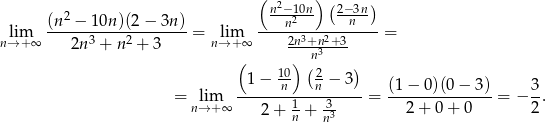
Odpowiedź: D
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Nieskończony ciąg liczbowy jest określony wzorem 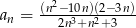 dla
dla 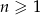 . Wtedy
. Wtedy
A) 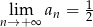 B)
B) 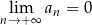 C)
C) 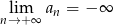 D)
D) 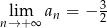
Liczymy (dzielimy licznik i mianownik przez 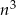 ).
).
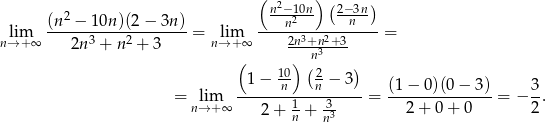
Odpowiedź: D
