/Szkoła średnia/Zadania maturalne/Matura 2017
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 1 kwietnia 2017 Czas pracy: 180 minut
Zadania zamknięte
W rozwinięciu wyrażenia 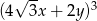 współczynnik przy iloczynie
współczynnik przy iloczynie 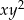 jest równy
jest równy
A) 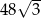 B) 288 C)
B) 288 C) 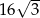 D) 144
D) 144
Na rysunku przedstawiony jest zbiór wszystkich liczb rzeczywistych spełniających nierówność 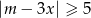 .
.
![]()
Stąd wynika, że
A) 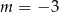 B)
B) 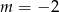 C)
C) 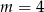 D)
D) 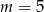
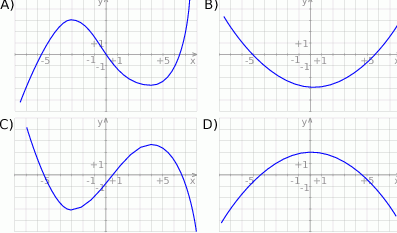
Rysunek przedstawia wykres funkcji 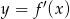 .
.
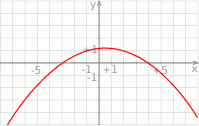
Wskaż wykres funkcji 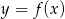 .
.
Ciąg 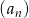 dla każdego
dla każdego 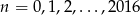 spełnia warunek
spełnia warunek 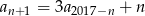 . Wyraz
. Wyraz 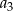 tego ciągu jest równy
tego ciągu jest równy
A) 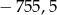 B)
B) 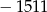 C)
C) 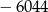 D)
D) 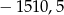
Granica 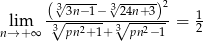 . Wynika stąd, że
. Wynika stąd, że
A) 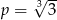 B)
B) 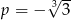 C)
C) 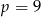 D)
D) 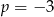
Zadania otwarte
Dany jest nieskończony ciąg geometryczny 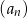 określony dla
określony dla 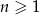 , w którym iloraz jest dwa razy większy od pierwszego wyrazu, a suma wszystkich wyrazów tego ciągu jest równa 14. Oblicz pierwszy wyraz tego ciągu.
, w którym iloraz jest dwa razy większy od pierwszego wyrazu, a suma wszystkich wyrazów tego ciągu jest równa 14. Oblicz pierwszy wyraz tego ciągu.
Liczby 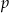 i
i 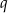 są pierwiastkami równania
są pierwiastkami równania 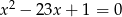 . Wykaż, że wartość wyrażenia
. Wykaż, że wartość wyrażenia 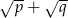 jest liczbą naturalną.
jest liczbą naturalną.
Wyznacz współrzędne środka okręgu, który jest obrazem okręgu o równaniu 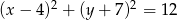 w jednokładności o środku
w jednokładności o środku 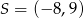 i skali
i skali 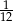 .
.
Oblicz promień okręgu opisanego na trapezie równoramiennym, w którym sinus kąta ostrego jest równy  , a przekątna ma długość 12.
, a przekątna ma długość 12.
Wykaż, że dla każdej liczby naturalnej  liczba
liczba 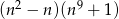 jest podzielna przez 6.
jest podzielna przez 6.
Rozwiąż nierówność 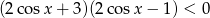 w przedziale
w przedziale 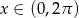 .
.
O zdarzeniach losowych 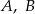 wiadomo, że:
wiadomo, że: 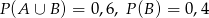 i
i 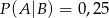 . Oblicz prawdopodobieństwo warunkowe
. Oblicz prawdopodobieństwo warunkowe 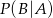 .
.
Na bokach 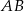 i
i 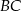 prostokąta
prostokąta 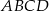 wybrano punkty
wybrano punkty 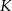 i
i 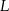 w ten sposób, że trójkąt
w ten sposób, że trójkąt 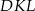 jest ostrokątny oraz
jest ostrokątny oraz 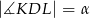 . Odcinek
. Odcinek 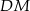 jest wysokością trójkąta
jest wysokością trójkąta 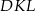 .
.
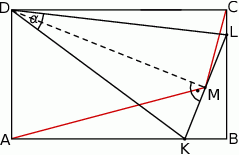
Wykaż, że 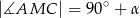 .
.
Dany jest ciąg 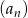 określony dla każdej liczby całkowitej
określony dla każdej liczby całkowitej 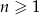 , w którym dla każdej liczby
, w którym dla każdej liczby 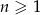 prawdziwe są równości
prawdziwe są równości
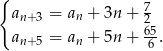
Wykaż, że ciąg 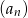 jest ciągiem rosnącym.
jest ciągiem rosnącym.
Rozwiąż nierówność 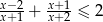 .
.
Oblicz, ile jest wszystkich liczb naturalnych sześciocyfrowych, w których zapisie występują co najmniej trzy cyfry nieparzyste.
W ostrosłup prawidłowy czworokątny wpisano sześcian tak, że jego cztery wierzchołki należą do wysokości ścian bocznych ostrosłupa, a pozostałe do płaszczyzny podstawy. Oblicz stosunek objętości ostrosłupa do objętości sześcianu jeżeli kąt nachylenia ściany bocznej do płaszczyzny podstawy jest równy  .
.
Rozpatrujemy wszystkie prostokąty 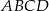 , których dwa wierzchołki
, których dwa wierzchołki 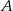 i
i 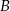 leżą na odcinku o końcach
leżą na odcinku o końcach 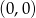 i
i 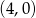 , a dwa pozostałe wierzchołki
, a dwa pozostałe wierzchołki 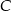 i
i 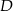 leżą na paraboli o równaniu
leżą na paraboli o równaniu 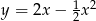 (zobacz rysunek).
(zobacz rysunek).
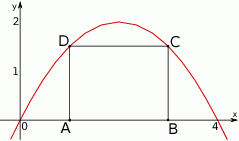
Oblicz obwód tego z rozpatrywanych prostokątów, którego pole jest największe.

