Zadanie nr 2318465

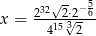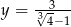Sprawdź, która liczba jest większa: 32√ - −5 x = 2-152⋅ 3√2-6- 4 2 , czy y = √33-- 4−1 .

Rozwiązanie

Uprośćmy najpierw pierwszą z liczb

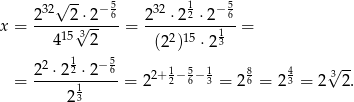
32√ -- − 5 32 1 − 5 x = 2----2√⋅2--6 = 2--⋅22-⋅2--6-= 415 32 (22)15 ⋅2 13 1 5 2-2 ⋅22-⋅2−-6 2+ 1−5− 1 8 4 √3-- = 1 = 2 2 6 3 = 2 6 = 23 = 2 2 . 23

Porównanie liczb i 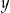przeprowadzimy na 2 sposoby.

Sposób I

Sprawdzamy, czy prawdziwa jest nierówność (wybieramy ją losowo).

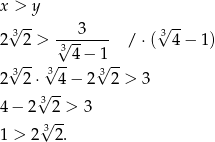
x > y √3-- 3 3√ -- 2 2 > √3------ /⋅ ( 4− 1) √ -- √ --4 −√1-- 2 32 ⋅ 34 − 2 32 > 3 √3-- 4 − 2 2 > 3 3√ -- 1 > 2 2.

Ta nierówność jest oczywiście sprzeczna, więc 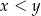x < y .

Sposób II

Usuńmy niewymierność z mianownika w deﬁnicji 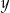– korzystamy ze wzoru na różnicę sześcianów.

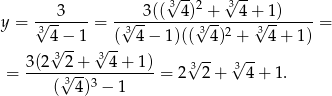
3√ --2 3√ -- y = √--3----= -√--3((--4)√+----4+√-1)-----= 34 − 1 ( 3 4− 1)(( 3 4)2 + 3 4+ 1) √3-- √3-- √ -- √ -- = 3(2-√2-+---4-+-1)-= 2 3 2+ 3 4+ 1. ( 34 )3 − 1

Teraz jest jasne, że 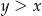y > x .