Zadanie nr 8309078
Rozwiązaniem równania 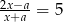 jest
jest 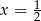 . Zatem
. Zatem
A) 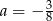 B)
B) 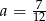 C)
C) 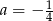 D)
D) 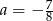
Rozwiązanie
Sposób I
Podstawiamy 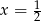 w danym równaniu.
w danym równaniu.
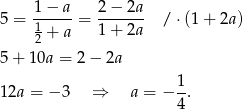
Sposób II
Przekształćmy najpierw dane równanie
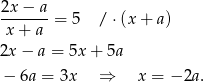
Mamy zatem
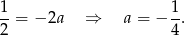
Odpowiedź: C
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Rozwiązaniem równania 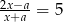 jest
jest 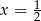 . Zatem
. Zatem
A) 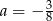 B)
B) 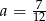 C)
C) 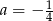 D)
D) 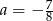
Sposób I
Podstawiamy 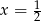 w danym równaniu.
w danym równaniu.
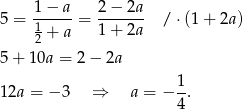
Sposób II
Przekształćmy najpierw dane równanie
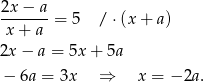
Mamy zatem
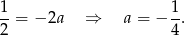
Odpowiedź: C
