/Szkoła średnia/Zadania maturalne/Matura 2018/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 21 kwietnia 2018 Czas pracy: 180 minut
Zadania zamknięte
Liczba 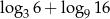 jest równa
jest równa
A) 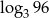 B)
B) 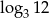 C)
C) 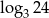 D)
D) 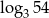
Nieskończony ciąg liczbowy jest określony wzorem 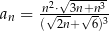 dla
dla 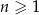 . Wtedy
. Wtedy
A) 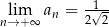 B)
B) 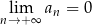 C)
C) 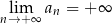 D)
D) 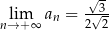
Rysunek przedstawia wykres funkcji 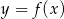 .
.
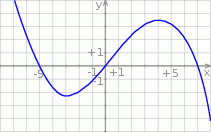
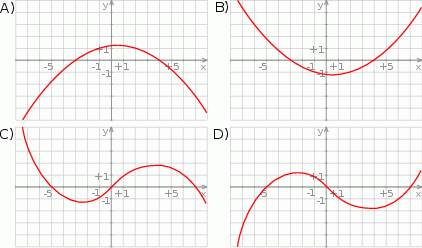
Wskaż wykres funkcji 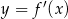 .
.
W trójkącie równoramiennym 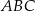 o podstawie
o podstawie 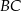 dane są:
dane są: 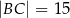 oraz
oraz 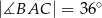 . Odcinek
. Odcinek 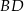 jest odcinkiem dwusiecznej kąta
jest odcinkiem dwusiecznej kąta  (zobacz rysunek).
(zobacz rysunek).
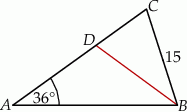
Wówczas długość odcinka 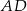 jest równa
jest równa
A) 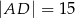 B)
B) 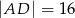 C)
C) 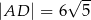 D)
D) 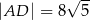
Dany jest nieskończony ciąg geometryczny, w którym iloraz jest trzy razy mniejszy od pierwszego wyrazu, a suma wszystkich wyrazów tego ciągu jest równa 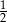 . Pierwszy wyraz tego ciągu jest równy
. Pierwszy wyraz tego ciągu jest równy
A) 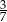 B)
B) 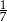 C)
C)  D) 7
D) 7
Zadania otwarte
Funkcja 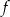 jest określona wzorem
jest określona wzorem 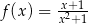 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równanie stycznej do wykresu tej funkcji w punkcie
. Wyznacz równanie stycznej do wykresu tej funkcji w punkcie 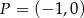 .
.
Okrąg przecina boki czworokąta 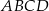 kolejno w punktach
kolejno w punktach 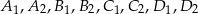 (zobacz rysunek).
(zobacz rysunek).
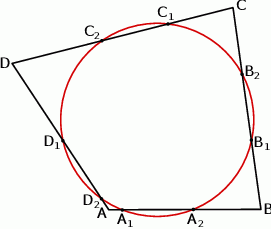
Wykaż, że jeżeli 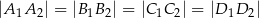 , to w czworokąt
, to w czworokąt 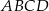 można wpisać okrąg.
można wpisać okrąg.
Oblicz jaka może być najmniejsza możliwa długość boku 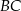 trójkąta
trójkąta 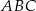 jeżeli
jeżeli 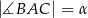 i pole trójkąta
i pole trójkąta 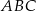 jest równe
jest równe 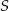 .
.
Wyznacz wszystkie wartości parametru 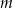 , dla których równanie
, dla których równanie 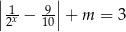 ma dokładnie jedno rozwiązanie i rozwiązanie to jest liczbą dodatnią. Wyznacz to rozwiązanie.
ma dokładnie jedno rozwiązanie i rozwiązanie to jest liczbą dodatnią. Wyznacz to rozwiązanie.
Udowodnij, że dla każdych dwóch liczb rzeczywistych 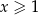 i
i 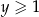 prawdziwa jest nierówność
prawdziwa jest nierówność
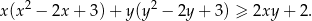
Wyznacz wszystkie rozwiązania równania 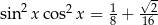 należące do przedziału
należące do przedziału 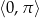 .
.
Suma 2018 początkowych wyrazów ciągu geometrycznego 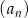 jest równa 1417, a suma odwrotności tych wyrazów jest równa 109. Oblicz iloczyn 2018 początkowych wyrazów ciągu
jest równa 1417, a suma odwrotności tych wyrazów jest równa 109. Oblicz iloczyn 2018 początkowych wyrazów ciągu 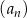 .
.
Napisz równanie okręgu o środku 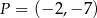 , którego punkty wspólne z okręgiem o równaniu
, którego punkty wspólne z okręgiem o równaniu 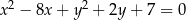 są końcami odcinka o długości
są końcami odcinka o długości 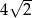 .
.
Z cyfr 0, 1, 2 tworzymy sześciocyfrowe liczby całkowite dodatnie podzielne przez 60. Oblicz, ile możemy utworzyć takich liczb.
W ostrosłupie prawidłowym czworokątnym ściana boczna jest nachylona do płaszczyzny podstawy pod kątem 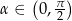 , a krawędź podstawy ma długość
, a krawędź podstawy ma długość  . Przez krawędź podstawy poprowadzono płaszczyznę tworzącą z płaszczyzna podstawy kąt
. Przez krawędź podstawy poprowadzono płaszczyznę tworzącą z płaszczyzna podstawy kąt 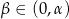 . Wykaż, że pole otrzymanego przekroju jest równe
. Wykaż, że pole otrzymanego przekroju jest równe
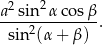
Na rysunku poniżej przedstawiono fragment wykresu funkcji 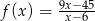 określonej dla
określonej dla 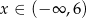 . Wykres ten przecina osie
. Wykres ten przecina osie 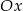 i
i 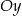 odpowiednio w punktach
odpowiednio w punktach 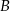 i
i 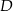 , a punkt
, a punkt 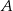 jest początkiem układu współrzędnych. Rozpatrujemy wszystkie czworokąty
jest początkiem układu współrzędnych. Rozpatrujemy wszystkie czworokąty 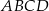 , w których punkt
, w których punkt 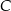 leży na wykresie funkcji
leży na wykresie funkcji 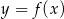 pomiędzy punktami
pomiędzy punktami 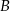 i
i 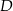 .
.
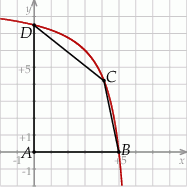
Oblicz współrzędne wierzchołka 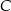 tego z rozpatrywanych czworokątów, którego pole jest największe.
tego z rozpatrywanych czworokątów, którego pole jest największe.

