/Szkoła średnia/Zadania maturalne/Matura 2018/Matura próbna/Zadania.info
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 14 kwietnia 2018 Czas pracy: 180 minut
Zadania zamknięte
Równanie 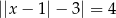 ma dokładnie
ma dokładnie
A) dwa rozwiązania rzeczywiste.
B) jedno rozwiązanie rzeczywiste.
C) cztery rozwiązania rzeczywiste.
D) trzy rozwiązania rzeczywiste.
Granica 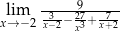
A) jest równa 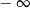 B) jest równa
B) jest równa 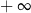 C) nie istnieje D) jest równa 0
C) nie istnieje D) jest równa 0
Liczba 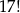 jest podzielna przez
jest podzielna przez
A) 71 B) 61 C) 51 D) 41
Dane są punkty 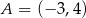 i
i 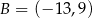 . Punkt
. Punkt 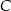 należący do odcinka
należący do odcinka 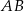 i taki, że
i taki, że 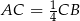 ma współrzędne
ma współrzędne
A) 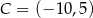 B)
B) 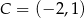 C)
C) 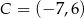 D)
D) 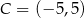
Funkcja 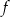 jest określona wzorem
jest określona wzorem 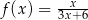 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 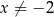 . Wówczas pochodna tej funkcji dla argumentu
. Wówczas pochodna tej funkcji dla argumentu 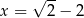 jest równa
jest równa
A) 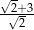 B)
B) 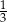 C)
C) 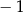 D)
D) 
Zadania otwarte
Pole trójkąta 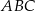 jest równe
jest równe 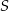 , a długości jego boków
, a długości jego boków 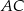 i
i 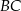 są odpowiednio równe
są odpowiednio równe 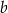 i
i  . Na bokach
. Na bokach 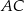 i
i 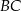 zbudowano kwadraty o środkach odpowiednio
zbudowano kwadraty o środkach odpowiednio 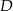 i
i 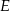 .
.
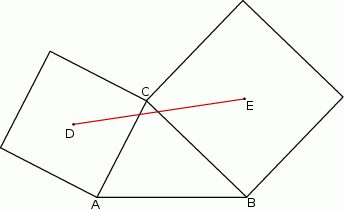
Wykaż, że
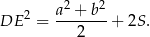
Wyznacz wszystkie liczby rzeczywiste 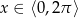 , dla których
, dla których
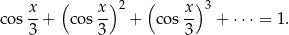
Udowodnij, że jeżeli 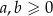 , to prawdziwa jest nierówność
, to prawdziwa jest nierówność 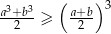 .
.
Na bokach 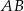 ,
, 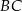 i
i 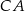 trójkąta
trójkąta 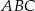 wybrano odpowiednio punkty
wybrano odpowiednio punkty 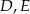 i
i 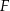 . Wykaż, że okręgi opisane na trójkątach
. Wykaż, że okręgi opisane na trójkątach 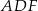 ,
, 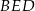 i
i 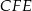 przecinają się w jednym punkcie.
przecinają się w jednym punkcie.
Ciąg 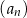 jest określony rekurencyjnie w następujący sposób
jest określony rekurencyjnie w następujący sposób
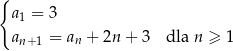
Oblicz ile wyrazów tego ciągu jest mniejszych niż 2018.
Wykaż, że
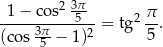
Spośród liczb naturalnych sześciocyfrowych wybieramy jedną liczbę. Jakie jest prawdopodobieństwo wybrania liczby, której iloczyn cyfr jest podzielny przez 9, jeżeli wiadomo, że każda cyfra wylosowanej liczby jest większa od 1?
Wykaż, że punkt o współrzędnych 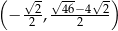 jest wierzchołkiem kwadratu opisanego na okręgu o równaniu
jest wierzchołkiem kwadratu opisanego na okręgu o równaniu
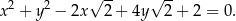
Na środkowej 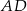 podstawy
podstawy 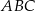 ostrosłupa trójkątnego
ostrosłupa trójkątnego 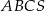 wybrano punkty
wybrano punkty 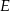 i
i 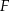 w ten sposób, że
w ten sposób, że 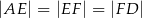 . Przez punkty
. Przez punkty 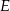 i
i 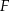 poprowadzono płaszczyzny równoległe do ściany
poprowadzono płaszczyzny równoległe do ściany 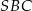 . Oblicz stosunek pól otrzymanych w ten sposób przekrojów ostrosłupa.
. Oblicz stosunek pól otrzymanych w ten sposób przekrojów ostrosłupa.
Wyznacz wszystkie wartości parametru 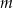 , dla których równanie
, dla których równanie
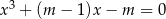
ma dokładnie dwa pierwiastki rzeczywiste. Dla otrzymanych wartości 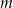 wyznacz te pierwiastki.
wyznacz te pierwiastki.
Rozpatrujemy prostokąty 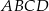 , których dwa wierzchołki leżą na osi
, których dwa wierzchołki leżą na osi 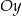 , jeden wierzchołek leży na paraboli określonej równaniem
, jeden wierzchołek leży na paraboli określonej równaniem 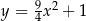 , jeden wierzchołek leży na wykresie funkcji
, jeden wierzchołek leży na wykresie funkcji 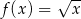 określonej dla
określonej dla 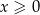 . Oblicz pole tego z tych prostokątów, który ma najmniejszy możliwy obwód.
. Oblicz pole tego z tych prostokątów, który ma najmniejszy możliwy obwód.