/Szkoła średnia/Zadania maturalne/Matura 2019
Próbny Egzamin Maturalny
z Matematyki (CEN Bydgoszcz)
poziom rozszerzony 7 marca 2019 Czas pracy: 180 minut
Zadania zamknięte
Granica 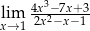 jest równa
jest równa
A) 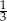 B)
B)  C)
C) 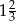 D)
D) 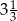
Zbiorem rozwiązań nierówności 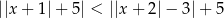 jest
jest
A) 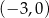 B)
B) 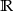 C)
C) 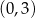 D)
D) 
Funkcja 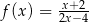 jest określona dla każdej liczby rzeczywistej
jest określona dla każdej liczby rzeczywistej 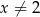 . Wówczas pochodna tej funkcji dla argumentu
. Wówczas pochodna tej funkcji dla argumentu 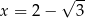 jest równa
jest równa
A)  B)
B) 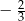 C)
C) 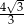 D)
D) 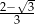
Dla dowolnej liczby rzeczywistej 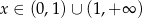 zachodzi zależność
zachodzi zależność 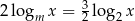 . Wartość parametru
. Wartość parametru 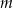 jest równa
jest równa
A)  B)
B) 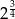 C)
C) 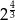 D)
D) 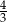
W trójkącie 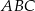 dane są wierzchołki
dane są wierzchołki 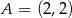 ,
, 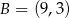 ,
, 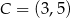 . Trójkąt
. Trójkąt 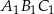 jest obrazem trójkąta
jest obrazem trójkąta 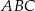 w jednokładności o środku
w jednokładności o środku 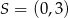 i skali
i skali 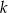 . Trójkąty te leżą po przeciwnych stronach osi rzędnych. Promień okręgu opisanego na trójkącie
. Trójkąty te leżą po przeciwnych stronach osi rzędnych. Promień okręgu opisanego na trójkącie 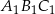 ma długość
ma długość 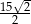 . Skala jednokładności
. Skala jednokładności 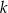 wynosi
wynosi
A) 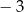 B)
B) 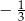 C)
C) 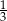 D) 3
D) 3
Zadania otwarte
Ze zbioru liczb 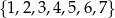 losujemy kolejno bez zwracania dwie. Oblicz prawdopodobieństwo, że suma wylosowanych liczb jest podzielna przez 3, jeżeli pierwsza z wylosowanych liczb jest liczbą pierwszą.
losujemy kolejno bez zwracania dwie. Oblicz prawdopodobieństwo, że suma wylosowanych liczb jest podzielna przez 3, jeżeli pierwsza z wylosowanych liczb jest liczbą pierwszą.
Wyznacz zbiór wartości funkcji 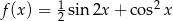 , gdzie
, gdzie 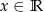 .
.
Dwa boki trójkąta ostrokątnego wpisanego w okrąg o promieniu 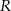 mają długości
mają długości 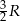 i
i 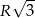 . Wykaż, że długość trzeciego boku wynosi
. Wykaż, że długość trzeciego boku wynosi 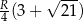 .
.
Ciąg 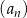 jest geometryczny o wyrazie pierwszym równym
jest geometryczny o wyrazie pierwszym równym 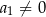 i ilorazie
i ilorazie 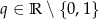 , Oblicz sumę
, Oblicz sumę 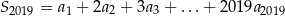 .
.
Wielomian 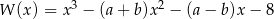 jest podzielny przez dwumian
jest podzielny przez dwumian 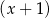 , a reszta z dzielenia wielomianu
, a reszta z dzielenia wielomianu 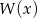 przez dwumian
przez dwumian 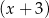 wynosi
wynosi 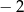 . Oblicz
. Oblicz  i
i 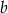 , a następnie rozwiąż nierówność
, a następnie rozwiąż nierówność 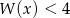 .
.
W trapez można wpisać okrąg o promieniu 4 i jednocześnie na tym trapezie można opisać okrąg. Kąt ostry trapezu ma miarę 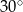 . Oblicz promień okręgu opisanego na tym trapezie.
. Oblicz promień okręgu opisanego na tym trapezie.
Wykaż, że zbiór 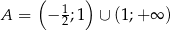 jest zbiorem wartości funkcji
jest zbiorem wartości funkcji
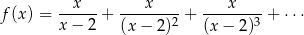
Dla jakich wartości parametru 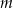 suma odwrotności pierwiastków równania
suma odwrotności pierwiastków równania
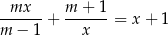
jest nie większa od 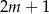 ?
?
Na krzywej 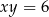 obrano punkty
obrano punkty 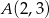 i
i 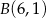 . Znajdź na tej krzywej taki punkt
. Znajdź na tej krzywej taki punkt 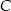 o ujemnej odciętej, aby pole trójkąta
o ujemnej odciętej, aby pole trójkąta 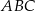 było najmniejsze.
było najmniejsze.
Dany jest ostrosłup prawidłowy czworokątny o krawędzi podstawy 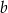 i kącie nachylenia krawędzi bocznej do krawędzi podstawy
i kącie nachylenia krawędzi bocznej do krawędzi podstawy  . Oblicz pole przekroju płaszczyzną przechodzącą przez wierzchołek i równoległą do krawędzi podstawy oraz nachyloną do płaszczyzny podstawy pod kątem
. Oblicz pole przekroju płaszczyzną przechodzącą przez wierzchołek i równoległą do krawędzi podstawy oraz nachyloną do płaszczyzny podstawy pod kątem 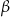 . Podaj konieczne założenia dotyczące kąta
. Podaj konieczne założenia dotyczące kąta  .
.
W pierwszej urnie są 4 kule zielone i 5 czerwonych, w drugiej urnie 3 zielone i 6 czerwonych. Z pierwszej urny losujemy jedną kulę i przekładamy ją do drugiej urny. Następnie do drugiej urny dokładamy 2 kule tego samego koloru co wylosowana kula. Losujemy dwie kule z drugiej urny. Oblicz prawdopodobieństwo, że obie będą zielone.

