/Szkoła średnia/Prawdopodobieństwo/Z definicji/Kostki

Zadanie nr 8130505

Dodaj do ulubionych
Dodaj do rozwiązanych

Rzucamy czterokrotnie symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że otrzymamy dokładnie dwie dwójki lub dokładnie dwie piątki. Wynik zapisz w postaci ułamka zwykłego nieskracalnego.

Rozwiązanie

Z zdarzenia elementarne przyjmujemy czteroelementowe ciągi otrzymanych liczb oczek. Mamy więc

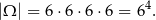
|Ω | = 6⋅6 ⋅6 ⋅6 = 64.

Dwójki i piątki pełnią dokładnie taką samą rolę, więc jest dokładnie tyle samo zdarzeń z dwoma dwójkami, co z dwoma piątkami. Miejsca dla dwóch dwójek (lub piątek) możemy wybrać na

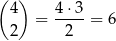
( ) 4 4⋅ 3 = ---- = 6 2 2

sposobów, a potem każdy z dwóch pozostałych wyników możemy wybrać na 5 sposobów. Jest więc

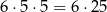
6⋅5 ⋅5 = 6 ⋅25

zdarzeń z dwoma dwójkami i tyle samo zdarzeń z dwoma piątkami.

Teraz trzeba jednak odrobinę uważać, bo niektóre zdarzenia policzyliśmy dwukrotnie: są to zdarzenia w których są zarówno 2 dwójki jak i 2 piątki. Takich zdarzeń jest 6:

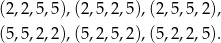
(2,2,5,5),(2,5,2,5),(2,5 ,5 ,2), (5,5,2,2),(5,2,5,2),(5,2 ,2 ,5).

Interesujące nas prawdopodobieństwo jest więc równe

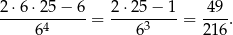
2-⋅6⋅2-5−--6 2-⋅25-−-1 -49- 64 = 63 = 216 .

 
Odpowiedź: -49 216

Wersja PDF