/Szkoła średnia/Zadania maturalne/Matura 2020
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom rozszerzony 18 kwietnia 2020 Czas pracy: 180 minut
Zadania zamknięte
Dla dowolnych liczb 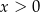 ,
, 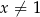 ,
, 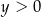 ,
, 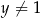 wartość wyrażenia
wartość wyrażenia 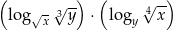 jest równa
jest równa
A) 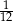 B)
B) 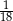 C)
C) 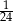 D)
D) 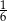
Która z poniższych funkcji jest rosnąca w zbiorze 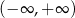 ?
?
A) 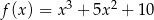 B)
B) 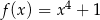
C) 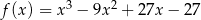 D)
D) 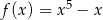
Wiadomo, że wśród pierwiastków wielomianu 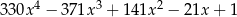 są odwrotności czterech różnych liczb pierwszych. Mediana wszystkich pierwiastków tego wielomianu jest równa
są odwrotności czterech różnych liczb pierwszych. Mediana wszystkich pierwiastków tego wielomianu jest równa
A) 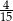 B)
B) 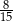 C)
C) 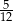 D)
D) 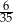
Boki równoległoboku  mają długości 2 i 5, a jego dłuższa przekątna ma długość 6.
mają długości 2 i 5, a jego dłuższa przekątna ma długość 6.
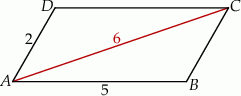
Pole tego równoległoboku jest równe
A) 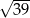 B) 48 C)
B) 48 C) 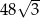 D)
D) 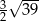
Zbiorem rozwiązań nierówności 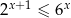 jest przedział
jest przedział
A) 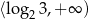 B)
B) 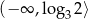 C)
C) 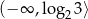 D)
D) 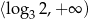
Zadania otwarte
Oblicz granicę 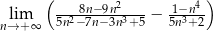 .
.
Dana jest funkcja 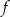 określona wzorem
określona wzorem 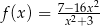 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Oblicz wartość
. Oblicz wartość 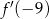 pochodnej tej funkcji dla argumentu
pochodnej tej funkcji dla argumentu 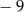 .
.
Dany jest nieskończony ciąg geometryczny 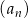 określony dla
określony dla 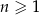 , w którym
, w którym 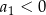 . Suma
. Suma 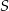 wszystkich wyrazów tego ciągu jest skończona i spełnia nierówność
wszystkich wyrazów tego ciągu jest skończona i spełnia nierówność 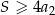 . Wyznacz iloraz tego ciągu.
. Wyznacz iloraz tego ciągu.
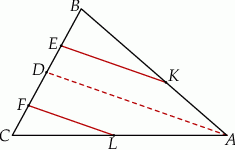
Na bokach 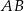 i
i 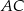 trójkąta
trójkąta 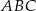 wybrano odpowiednio punkty
wybrano odpowiednio punkty 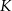 i
i 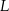 w ten sposób, że
w ten sposób, że 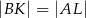 . Punkt
. Punkt 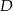 jest środkiem odcinka
jest środkiem odcinka 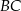 . Przez punkty
. Przez punkty 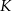 i
i 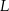 poprowadzono proste równoległe do
poprowadzono proste równoległe do 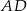 , które wyznaczyły na boku
, które wyznaczyły na boku 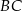 punkty
punkty 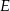 i
i 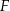 odpowiednio (zobacz rysunek). Wykaż, że jeżeli
odpowiednio (zobacz rysunek). Wykaż, że jeżeli 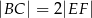 , to
, to 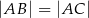 .
.
Funkcja 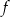 jest wielomianem stopnia 3, a jej wykres znajduje się powyżej osi
jest wielomianem stopnia 3, a jej wykres znajduje się powyżej osi 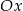 na zbiorze
na zbiorze 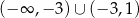 . Wyznacz równanie stycznej do wykresu funkcji
. Wyznacz równanie stycznej do wykresu funkcji 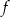 w punkcie
w punkcie 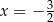 jeżeli wiadomo, że styczna ta jest równoległa do prostej
jeżeli wiadomo, że styczna ta jest równoległa do prostej 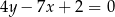 .
.
Wykaż, że 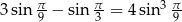 .
.
Czterdzieści osób usadzono w sposób losowy przy czterech dziesięcioosobowych okrągłych stołach. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że trzy ustalone wcześniej osoby siedzą przy jednym stole.
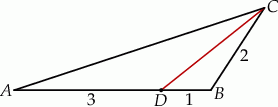
Na boku 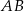 trójkąta
trójkąta 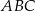 wybrano punkt
wybrano punkt 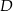 w ten sposób, że
w ten sposób, że 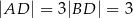 . Bok
. Bok 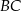 tego trójkąta ma długość 2. Oblicz stosunek długości odcinków
tego trójkąta ma długość 2. Oblicz stosunek długości odcinków 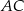 i
i 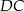 .
.
Punkt 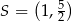 leży wewnątrz figury
leży wewnątrz figury 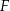 opisanej układem nierówności
opisanej układem nierówności
Wyznacz równanie największego okręgu o środku  , który jest zawarty wewnątrz figury
, który jest zawarty wewnątrz figury  .
.
Wielomian określony wzorem 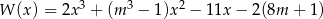 jest podzielny przez dwumian
jest podzielny przez dwumian 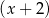 oraz przy dzieleniu przez dwumian
oraz przy dzieleniu przez dwumian 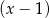 daje resztę 12. Oblicz
daje resztę 12. Oblicz 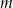 i dla wyznaczonej wartości
i dla wyznaczonej wartości 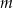 rozwiąż nierówność
rozwiąż nierówność 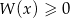 .
.
Objętość graniastosłupa prawidłowego trójkątnego jest równa 8, a przekątne dwóch ścian bocznych poprowadzone z jednego wierzchołka tworzą kąt  . Oblicz długość krawędzi podstawy tego graniastosłupa.
. Oblicz długość krawędzi podstawy tego graniastosłupa.
Rozpatrujemy trapezy równoramienne 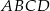 o przekątnej długości 1 i sumie długości podstaw równej
o przekątnej długości 1 i sumie długości podstaw równej  . Zapisz pole trapezu
. Zapisz pole trapezu 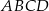 jako funkcję zmiennej
jako funkcję zmiennej  . Wyznacz dziedzinę tej funkcji i oblicz sumę długości podstaw tego z rozważanych trapezów, którego pole jest największe. Oblicz to największe pole.
. Wyznacz dziedzinę tej funkcji i oblicz sumę długości podstaw tego z rozważanych trapezów, którego pole jest największe. Oblicz to największe pole.

