/Szkoła średnia/Zadania maturalne/Matura 2020/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom rozszerzony 25 kwietnia 2020 Czas pracy: 180 minut
Zadania zamknięte
Granica jednostronna 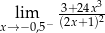 jest równa
jest równa
A) 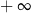 B) 9 C) 0 D)
B) 9 C) 0 D) 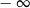
Liczba 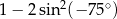 jest równa
jest równa
A) 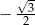 B)
B) 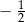 C)
C) 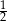 D)
D) 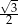
Suma rozwiązań równania 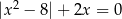 jest równa
jest równa
A) 0 B) 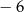 C) 2 D)
C) 2 D) 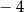
Nieskończony ciąg geometryczny 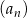 jest określony w następujący sposób:
jest określony w następujący sposób: 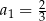 oraz
oraz 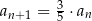 dla
dla 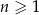 . Suma wszystkich wyrazów tego ciągu jest równa
. Suma wszystkich wyrazów tego ciągu jest równa
A)  B)
B) 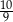 C)
C) 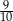 D)
D) 
Okrąg 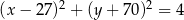 jest styczny do prostej
jest styczny do prostej
A) 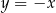 B)
B) 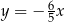 C)
C) 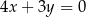 D)
D) 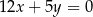
Zadania otwarte
Liczby rzeczywiste 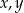 spełniają warunki:
spełniają warunki: 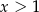 ,
, 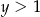 oraz
oraz 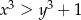 . Wykaż, że prawdziwa jest równość
. Wykaż, że prawdziwa jest równość
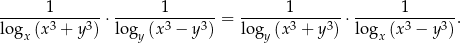
Rozważamy wszystkie liczby naturalne pięciocyfrowe zapisane przy użyciu cyfr 0, 3, 5, 7, 9, bez powtarzania jakiejkolwiek cyfry. Oblicz sumę wszystkich takich liczb.
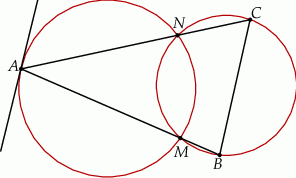
Dwa okręgi przecinają się w punktach 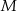 i
i 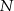 . Przez punkt
. Przez punkt 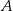 pierwszego okręgu prowadzimy proste
pierwszego okręgu prowadzimy proste 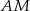 i
i 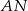 , przecinające drugi okrąg w punktach
, przecinające drugi okrąg w punktach 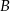 i
i 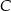 . Udowodnij, że styczna w punkcie
. Udowodnij, że styczna w punkcie 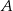 do pierwszego okręgu jest równoległa do prostej
do pierwszego okręgu jest równoległa do prostej 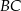 .
.
Udowodnij, że dla każdej liczby całkowitej 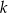 i dla każdej liczby całkowitej
i dla każdej liczby całkowitej 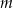 liczba
liczba 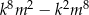 jest podzielna przez 36.
jest podzielna przez 36.
W pudełku znajdują się 4 kule czarne i 6 kul białych. Rzucamy dwa razy monetą. Jeśli otrzymamy 2 reszki, losujemy z pudełka kolejno bez zwracania 2 kule. W pozostałych przypadkach losujemy trzy kule. Oblicz prawdopodobieństwo, że wśród wylosowanych kul jest dokładnie jedna kula czarna.
W równoległoboku boki mają długości 3 i 7, a jedna z przekątnych ma długość 6. Oblicz cosinus kąta ostrego pod jakim przecinają się przekątne tego równoległoboku.
Rozwiąż równanie
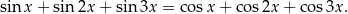
Przedłużenia ramion 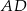 i
i 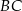 trapezu równoramiennego
trapezu równoramiennego 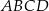 przecinają się w punkcie
przecinają się w punkcie 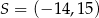 . Wyznacz współrzędne wierzchołków
. Wyznacz współrzędne wierzchołków 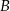 i
i 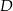 tego trapezu, jeżeli
tego trapezu, jeżeli 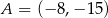 i
i 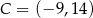 .
.
W ostrosłupie prawidłowym czworokątnym 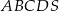 o podstawie
o podstawie 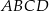 wysokość jest równa
wysokość jest równa 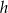 , a kąt między sąsiednimi ścianami bocznymi ostrosłupa ma miarę
, a kąt między sąsiednimi ścianami bocznymi ostrosłupa ma miarę  . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Wyznacz wszystkie wartości parametru 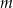 , dla których równanie
, dla których równanie
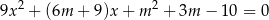
ma dwa różne ujemne rozwiązania 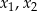 spełniające nierówność
spełniające nierówność 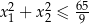 .
.
Z odcinka drutu o długości 4 m wykonano ramkę w kształcie rombu z jedną przekątną (zobacz rysunek).
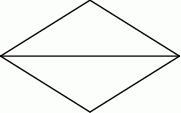
Jaka powinna być długość tej przekątnej, aby pole powierzchni tego rombu było największe możliwe?

