/Szkoła średnia/Zadania z treścią

Zadanie nr 5394102

Dodaj do ulubionych
Dodaj do rozwiązanych

Trasę etapu wyścigu kolarskiego o długości 150 km pan Nowak pokonał w czasie o 1 godzinę i 50 minut krótszym niż jego kolega z drużyny, pan Kowalski. Średnia wartość prędkości, z jaką pan Nowak jechał na tym etapie, była o 11 km/h większa od średniej wartości prędkości pana Kowalskiego na tej trasie. Oblicz średnie wartości prędkości, z jakimi przejechali całą trasę obaj zawodnicy.

Rozwiązanie

Sposób I

Niech 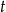t i v oznaczają odpowiednio czas przejazdu oraz prędkość pana Nowaka. Z podanych informacji mamy

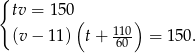
{ tv = 1 50 ( 110) (v − 11) t + -60- = 1 50.

Podstawiamy 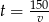t = 150- v z pierwszego równania do drugiego.

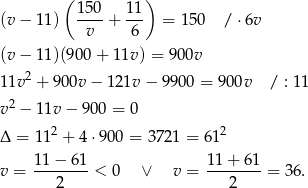
( ) 1-50 11- (v− 11) v + 6 = 1 50 / ⋅6v (v− 11)(900 + 11v ) = 900v 11v2 + 900v − 1 21v − 9900 = 900v / : 11 v2 − 11v − 900 = 0 2 2 Δ = 11 + 4⋅90 0 = 3721 = 61 1-1−-6-1 11-+-61- v = 2 < 0 ∨ v = 2 = 36.

Ujemne rozwiązanie odrzucamy i mamy 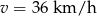v = 36 km/h . Wtedy prędkość pana Kowalskiego to

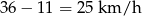
36 − 11 = 25 km/h

Sposób II

Wprowadzamy oznaczenia: 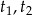t1,t2 niech oznaczają czas przejazdu pana Nowaka i Kowalskiego, a 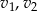v1,v2 niech oznaczają ich prędkości. Z założeń mamy

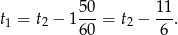
t1 = t2 − 1 50-= t2 − 11-. 60 6

Stąd

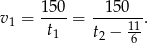
1 50 150 v1 = ---- = ----11. t1 t2 − -6

Podstawiamy to do równania

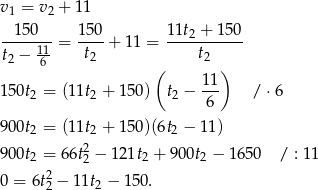
v1 = v 2 + 1 1 150 150 11t2 + 150 -----11 = ----+ 11 = ----------- t2 − 6 t2 ( t2 ) 11 150t2 = (1 1t2 + 15 0) t2 − --- /⋅ 6 6 900t2 = (1 1t2 + 15 0)(6t2 − 1 1) 2 900t2 = 6 6t2 − 12 1t2 + 90 0t2 − 16 50 / : 11 0 = 6t22 − 11t2 − 150.

Wyznaczamy pierwiastki

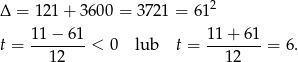
Δ = 1 21+ 3600 = 37 21 = 612 t = 11-−-61-< 0 lub t = 11-+-61-= 6. 1 2 1 2

Odrzucamy wynik ujemny i otrzymujemy 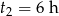t2 = 6 h . Obliczamy prędkość pana Kowalskiego

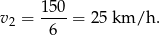
v = 150-= 2 5 km/h . 2 6

Teraz pozostało nam tylko obliczyć prędkość pana Nowaka

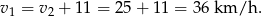
v1 = v 2 + 1 1 = 25 + 11 = 3 6 km/h .

 
Odpowiedź: Prędkość pana Nowaka: 36 km/h, pana Kowalskiego: 25 km/h

Wersja PDF