/Szkoła średnia/Zadania maturalne/Matura 2020/Matura próbna/CKE, OKE, CEN
Lubelska próba przed maturą
z matematyki (dla klas drugich)
poziom rozszerzony 14 maja 2019 Czas pracy: 180 minut
Zadania zamknięte
Dany jest ciąg geometryczny nieskończony
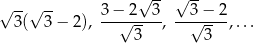
Suma wszystkich wyrazów tego ciągu jest równa
A) 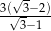 B)
B) 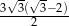 C) szereg jest rozbieżny D)
C) szereg jest rozbieżny D) 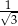
Granica 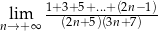 jest równa
jest równa
A) 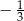 B)
B) 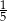 C)
C) 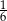 D) 0
D) 0
Równanie 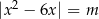 o niewiadomej
o niewiadomej  ma cztery rozwiązania dla
ma cztery rozwiązania dla 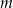
A) 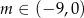 B)
B) 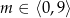 C)
C) 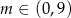 D)
D) 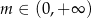
Zbiór 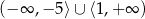 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności
A) 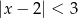 B)
B) 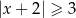 C)
C) 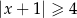 D)
D) 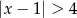
Wartość wyrażenia 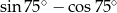 jest równa
jest równa
A) 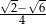 B)
B) 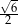 C)
C) 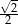 D) 0
D) 0
Zadania otwarte
Dla jakich wartości parametru 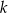 reszta z dzielenia wielomianu
reszta z dzielenia wielomianu
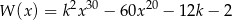
przez dwumian 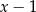 jest równa 2?
jest równa 2?
Dla jakich wartości parametru 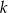 suma kwadratów pierwiastków równania
suma kwadratów pierwiastków równania 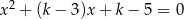 jest najmniejsza?
jest najmniejsza?
Rozwiąż nierówność 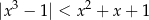 .
.
Trzy liczby tworzą rosnący ciąg geometryczny. Suma tych liczb jest równa 28. Liczby te są jednocześnie 1, 2 i 4 wyrazem ciągu arytmetycznego. Jakie to liczby?
Wykaż, że jeżeli 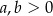 to
to 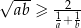 .
.
Wyznacz dziedzinę i zbiór wartości funkcji
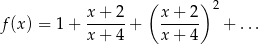
Naszkicuj wykres funkcji 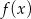 .
.
Wykaż, że punkt przecięcia przekątnych trapezu leży na prostej przechodzącej przez środki jego podstaw.
Rozwiąż równanie 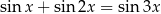 w przedziale
w przedziale 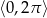 .
.
W trapezie opisanym na okręgu ramiona mają długości 6 i 10. Odcinek łączący środki tych ramion dzieli trapez na dwie części, których pola pozostają w stosunku 5:11. Wyznacz długości podstaw tego trapezu.
W romb o boku 8 i kącie ostrym 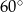 wpisano okrąg. Wyznacz pole prostokąta, którego wierzchołki leżą w punktach styczności okręgu z bokami rombu.
wpisano okrąg. Wyznacz pole prostokąta, którego wierzchołki leżą w punktach styczności okręgu z bokami rombu.

