/Szkoła średnia/Zadania maturalne/Matura 2020/Matura próbna/Zadania.info
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom podstawowy 7 marca 2020 Czas pracy: 170 minut
Zadania zamknięte
Liczba 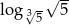 jest równa
jest równa
A) 3 B) 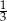 C)
C)  D)
D) 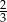
Liczba naturalna 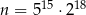 w zapisie dziesiętnym ma
w zapisie dziesiętnym ma
A) 16 cyfr B) 15 cyfr C) 18 cyfr D) 33 cyfry
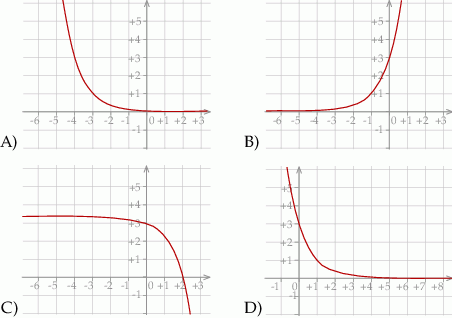
Wykres funkcji 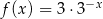 przedstawiony jest na rysunku:
przedstawiony jest na rysunku:
Liczba dodatnia  jest zapisana w postaci ułamka zwykłego o dodatnim mianowniku. Jeżeli licznik tego ułamka zwiększymy o 25%, a jego mianownik zmniejszymy o 25%, to otrzymamy liczbę
jest zapisana w postaci ułamka zwykłego o dodatnim mianowniku. Jeżeli licznik tego ułamka zwiększymy o 25%, a jego mianownik zmniejszymy o 25%, to otrzymamy liczbę 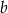 taką, że
taką, że
A) 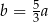 B)
B) 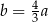 C)
C) 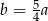 D)
D) 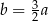
Układ liczb 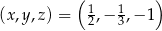 jest rozwiązaniem układu równań
jest rozwiązaniem układu równań
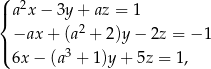
dla
A) 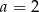 B)
B) 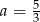 C)
C) 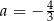 D)
D) 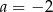
Równanie 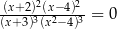
A) ma cztery różne rozwiązania: 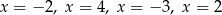 .
.
B) ma trzy różne rozwiązania: 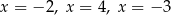 .
.
C) ma dwa różne rozwiązania: 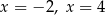 .
.
D) ma jedno rozwiązanie: 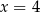 .
.
Funkcja 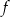 jest określona dla każdej liczby rzeczywistej
jest określona dla każdej liczby rzeczywistej  wzorem
wzorem 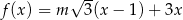 . Ta funkcja jest malejąca dla każdej liczby
. Ta funkcja jest malejąca dla każdej liczby 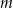 spełniającej warunek
spełniającej warunek
A) 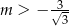 B)
B) 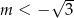 C)
C) 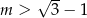 D)
D) 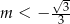
Na rysunku przedstawiono fragment paraboli będącej wykresem funkcji kwadratowej 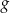 . Wierzchołkiem tej paraboli jest punkt
. Wierzchołkiem tej paraboli jest punkt 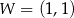 .
.
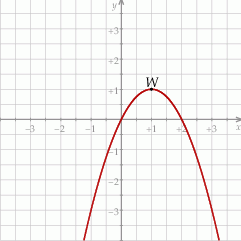
Zbiorem wartości funkcji 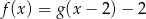 jest przedział
jest przedział
A) 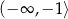 B)
B) 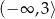 C)
C) 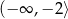 D)
D) 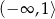
Zbiorem rozwiązań nierówności 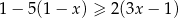 jest przedział
jest przedział
A) 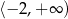 B)
B) 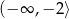 C)
C) 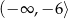 D)
D) 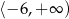
Poniższy diagram przedstawia wiek uczestników pewnej wycieczki.
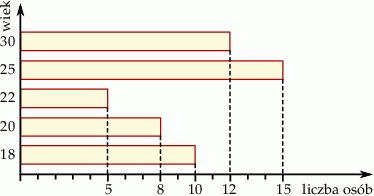
Mediana wieku osób uczestniczących w tej wycieczce jest równa:
A) 21 lat B) 22 lata C) 23,5 lat D) 25 lat
Liczba 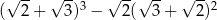 jest równa
jest równa
A) 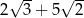 B)
B) 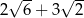 C)
C) 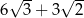 D)
D) 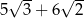
Dany jest ciąg geometryczny 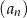 , określony dla
, określony dla 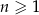 . Wszystkie wyrazy tego ciągu są dodatnie i spełniony jest warunek
. Wszystkie wyrazy tego ciągu są dodatnie i spełniony jest warunek 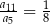 . Iloraz tego ciągu jest równy
. Iloraz tego ciągu jest równy
A) 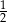 B)
B) 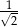 C)
C) 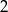 D)
D) 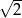
Dany jest ciąg arytmetyczny 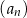 określony wzorem
określony wzorem 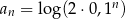 dla każdej liczby naturalnej
dla każdej liczby naturalnej 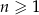 . Różnica
. Różnica  tego ciągu jest równa
tego ciągu jest równa
A) 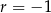 B)
B) 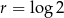 C)
C) 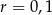 D)
D) 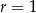
Wartość wyrażenia 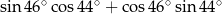 jest równa
jest równa
A) 1 B) 0 C) 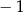 D) 2
D) 2
Odcinek 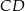 jest wysokością trójkąta równoramiennego
jest wysokością trójkąta równoramiennego 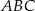 , w którym
, w którym 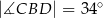 (zobacz rysunek). Okrąg o środku
(zobacz rysunek). Okrąg o środku 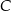 i promieniu
i promieniu 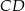 jest styczny do prostej
jest styczny do prostej 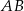 . Okrąg ten przecina boki
. Okrąg ten przecina boki 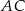 i
i 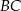 trójkąta odpowiednio w punktach
trójkąta odpowiednio w punktach 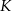 i
i 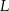 .
.
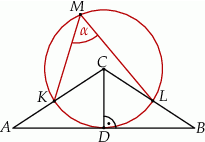
Zaznaczony na rysunku kąt  wpisany w okrąg jest równy
wpisany w okrąg jest równy
A) 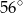 B)
B) 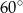 C)
C) 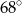 D)
D) 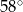
Czworokąt 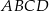 jest deltoidem (zobacz rysunek), w którym
jest deltoidem (zobacz rysunek), w którym 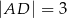 ,
, 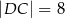 oraz
oraz 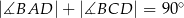 .
.
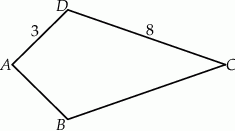
Pole tego deltoidu jest równe
A) 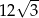 B)
B) 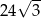 C)
C) 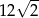 D)
D) 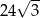
Prosta o równaniu 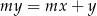 nie przecina prostej
nie przecina prostej 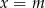 . Zatem
. Zatem
A) 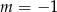 B)
B) 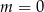 C)
C) 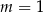 D)
D) 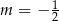
Suma odległości punktu 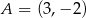 od prostych o równaniach
od prostych o równaniach 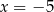 i
i 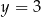 jest równa
jest równa
A) 5 B) 10 C) 13 D) 8
Punkty: 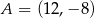 ,
, 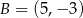 ,
, 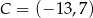 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku 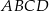 . Wierzchołek
. Wierzchołek 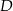 tego równoległoboku ma współrzędne
tego równoległoboku ma współrzędne
A) 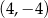 B)
B) 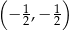 C)
C) 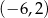 D)
D) 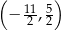
Dane są punkty o współrzędnych 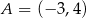 oraz
oraz 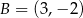 . Średnica okręgu opisanego na kwadracie o boku
. Średnica okręgu opisanego na kwadracie o boku 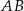 jest równa
jest równa
A) 12 B) 6 C) 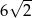 D)
D) 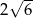
Podstawą graniastosłupa prostego jest prostokąt o bokach długości 3 i 4. Kąt  , jaki tworzą dwie przekątne tego graniastosłupa, jest równy
, jaki tworzą dwie przekątne tego graniastosłupa, jest równy 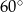 (zobacz rysunek).
(zobacz rysunek).
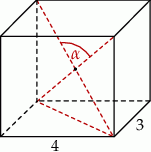
Wysokość graniastosłupa jest równa
A) 10 B) 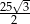 C)
C) 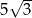 D)
D) 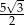
Podstawą ostrosłupa jest prostokąt 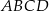 o bokach długości:
o bokach długości: 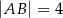 i
i 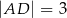 . Krawędź boczna
. Krawędź boczna 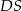 jest prostopadła do podstawy i ma długość 3 (zobacz rysunek).
jest prostopadła do podstawy i ma długość 3 (zobacz rysunek).
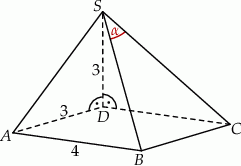
Jeżeli  jest katem pomiędzy krawędziami bocznymi
jest katem pomiędzy krawędziami bocznymi 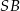 i
i 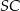 , to
, to
A) 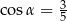 B)
B) 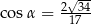 C)
C) 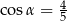 D)
D) 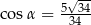
Pole powierzchni całkowitej pewnego stożka jest 4 razy większe od pola powierzchni pewnej kuli. Promień tej kuli jest równy 3 i jest taki sam jak promień podstawy tego stożka. Tworząca tego stożka ma długość równą
A) 42 B) 45 C) 48 D) 52
Ile jest nieujemnych liczb całkowitych mniejszych niż 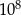 , które są zapisane wyłącznie przy użyciu cyfr 0, 1 i 2?
, które są zapisane wyłącznie przy użyciu cyfr 0, 1 i 2?
A) 19683 B) 59049 C) 6561 D) 512
Z grupy 72 osób (kobiet i mężczyzn) losujemy jedną osobę. Prawdopodobieństwo zdarzenia polegającego na tym, że wylosujemy mężczyznę, jest równe  . Liczba kobiet w tej grupie jest równa
. Liczba kobiet w tej grupie jest równa
A) 24 B) 48 C) 36 D) 12
Zadania otwarte
Rozwiąż nierówność 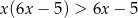 .
.
Rozwiąż równanie 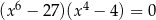 .
.
Wierzchołki 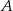 i
i 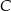 trójkąta
trójkąta 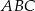 leżą na okręgu o promieniu
leżą na okręgu o promieniu  , a środek
, a środek 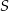 tego okręgu leży na boku
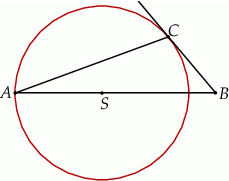
tego okręgu leży na boku 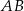 trójkąta (zobacz rysunek). Prosta
trójkąta (zobacz rysunek). Prosta 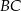 jest styczna do tego okręgu w punkcie
jest styczna do tego okręgu w punkcie 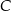 , a ponadto
, a ponadto 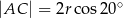 . Wykaż, że kąt
. Wykaż, że kąt 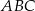 ma miarę
ma miarę 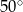 .
.
Na rysunku przedstawiono trójkąt 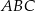 , w którym
, w którym 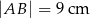 oraz odcinek
oraz odcinek 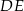 równoległy do boku
równoległy do boku 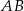 trójkąta.
trójkąta.
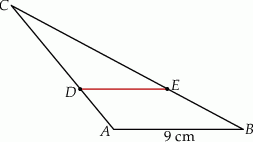
Stosunek pola trapezu 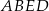 do pola trójkąta
do pola trójkąta 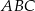 jest równy
jest równy 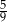 . Oblicz długość odcinka
. Oblicz długość odcinka 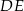 .
.
Wykaż, że dla dowolnych liczb rzeczywistych  i
i 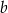 prawdziwa jest nierówność
prawdziwa jest nierówność
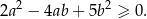
Doświadczenie losowe polega na trzykrotnym rzucie symetryczną sześcienną kostką do gry. Oblicz prawdopodobieństwo zdarzenia 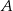 polegającego na tym, że iloczyn liczb oczek otrzymanych w trzech rzutach będzie podzielny przez 54.
polegającego na tym, że iloczyn liczb oczek otrzymanych w trzech rzutach będzie podzielny przez 54.
Ciąg geometryczny 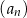 jest określony dla każdej liczby naturalnej
jest określony dla każdej liczby naturalnej 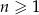 . Ilorazem tego ciągu jest liczba
. Ilorazem tego ciągu jest liczba 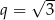 , a iloczyn 5 początkowych wyrazów tego ciągu:
, a iloczyn 5 początkowych wyrazów tego ciągu: 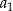 ,
, 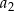 ,
, 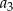 ,
, 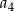 ,
, 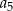 jest równy
jest równy 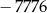 .
.
- Oblicz pierwszy wyraz tego ciągu.
- Oblicz sumę pierwszych ośmiu wyrazów tego ciągu.
Podstawą ostrosłupa jest prostokąt, którego stosunek długości boków wynosi 4:3. Pole podstawy ostrosłupa jest równe 48. Każda krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem 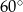 . Oblicz pole powierzchni bocznej tego ostrosłupa.
. Oblicz pole powierzchni bocznej tego ostrosłupa.
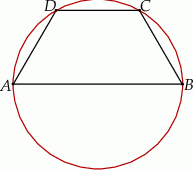
W okrąg wpisano trapez równoramienny 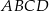 w ten sposób, że podstawa
w ten sposób, że podstawa 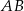 jest średnicą tego okręgu. Ramię trapezu ma długość 10, a jego przekątna jest o 11 dłuższa od promienia okręgu. Oblicz wysokość tego trapezu.
jest średnicą tego okręgu. Ramię trapezu ma długość 10, a jego przekątna jest o 11 dłuższa od promienia okręgu. Oblicz wysokość tego trapezu.