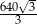/Szkoła średnia/Geometria/Stereometria/Ostrosłup/Dowolny/Czworokątny/Prostokąt w podstawie

Zadanie nr 5646218

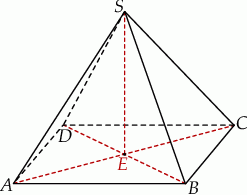
Podstawą ostrosłupa 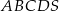ABCDS jest prostokąt, którego boki pozostają w stosunku 3:4, a pole jest równe 192 (zobacz rysunek). Punkt 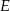E jest wyznaczony przez przecinające się przekątne podstawy, a odcinek 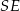SE jest wysokością ostrosłupa. Każda krawędź boczna tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem 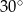∘ 30 . Oblicz objętość ostrosłupa.

PIC

Wersja PDF

Rozwiązanie

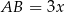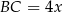Jeżeli oznaczymy AB = 3x i BC = 4x , to z podanego pola podstawy mamy

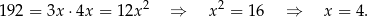
192 = 3x ⋅4x = 12x2 ⇒ x 2 = 16 ⇒ x = 4.

Wysokość ostrosłupa obliczymy z trójkąta prostokątnego 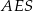AES , ale zanim to zrobimy obliczmy długość odcinka AE .

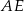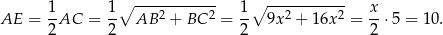
∘ ------------ ∘ ----------- AE = 1AC = 1- AB 2 + BC 2 = 1- 9x 2 + 1 6x2 = x-⋅5 = 10. 2 2 2 2

Obliczamy teraz z trójkąta 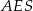AES wysokość ostrosłupa.

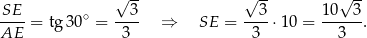
√ -- √ -- √ -- SE ∘ 3 3 10 3 ----= tg 30 = ---- ⇒ SE = ----⋅1 0 = ------. AE 3 3 3

Pozostało obliczyć objętość ostrosłupa.

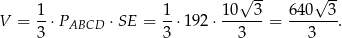
√ -- √ -- 1 1 10 3 640 3 V = -⋅ PABCD ⋅ SE = --⋅192 ⋅------= -------. 3 3 3 3

 
Odpowiedź: 640√3 3

Wersja PDF