/Szkoła średnia/Zadania maturalne/Matura 2021/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom rozszerzony 1 maja 2021 Czas pracy: 180 minut
Zadania zamknięte
Ile jest liczb naturalnych pięciocyfrowych, których iloczyn cyfr jest dodatnią liczbą złożoną?
A) 59029 B) 59028 C) 89980 D) 89979
Dana jest funkcja 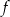 określona wzorem
określona wzorem 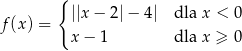
Równanie 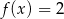 ma dokładnie
ma dokładnie
A) jedno rozwiązanie. B) dwa rozwiązania. C) cztery rozwiązania. D) pięć rozwiązań.
Pochodna funkcji 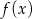 jest równa
jest równa 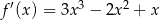 . Funkcja
. Funkcja 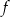 może mieć wzór
może mieć wzór
A) 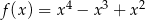 B)
B) 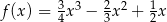
C) 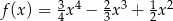 D)
D) 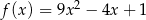
Granica 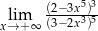 jest równa
jest równa
A) 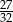 B)
B) 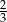 C)
C) 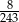 D)
D) 
Zadania otwarte
Niech 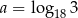 . Wykaż, że
. Wykaż, że 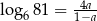 .
.
W fabryce obuwia pracuje pięć linii produkcyjnych produkujących ten sam model butów. W poniższej tabeli zawarto informacje o wydajności tych linii oraz o odsetku wadliwych par obuwia produkowanych przez każdą z nich.
| Linia produkcyjna | Wydajność | Odsetek wadliwych par |
| I | 60 par/godzinę | 2% |
| II | 50 par/godzinę | 3% |
| III | 40 par/godzinę | 1% |
| IV | 80 par/godzinę | 3% |
| V | 70 par/godzinę | 2% |
Wybieramy losowo jedną parę obuwia wyprodukowaną przez te linie produkcyjne. Jakie jest prawdopodobieństwo, że wybrana para nie okaże się wadliwa?
Wykaż, że jeżeli 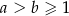 , to
, to 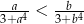 .
.
Rozwiąż równanie 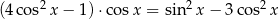 , dla
, dla 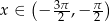 .
.
W trójkąt równoramienny 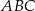 o podstawie długości
o podstawie długości 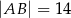 i polu 168 wpisano okrąg. Oblicz długość odcinka łączącego wierzchołek
i polu 168 wpisano okrąg. Oblicz długość odcinka łączącego wierzchołek 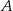 z punktem wspólnym okręgu i ramienia
z punktem wspólnym okręgu i ramienia 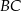 .
.
Wielomian 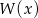 stopnia 3 jest podzielny przez trójmian kwadratowy
stopnia 3 jest podzielny przez trójmian kwadratowy 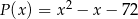 . Wiadomo ponadto, że
. Wiadomo ponadto, że 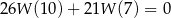 . Wyznacz miejsca zerowe wielomianu
. Wyznacz miejsca zerowe wielomianu 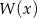 .
.
Przez każde dwa sąsiednie wierzchołki czworokąta 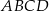 wpisanego w okrąg poprowadzono okrąg (zobacz rysunek).
wpisanego w okrąg poprowadzono okrąg (zobacz rysunek).
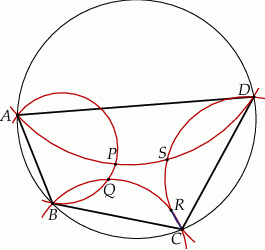
Wykaż, że punkty 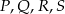 , w których przecinają się te okręgi, leżą na jednym okręgu.
, w których przecinają się te okręgi, leżą na jednym okręgu.
Współczynniki wielomianu 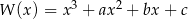 spełniają warunek:
spełniają warunek: 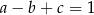 . Trzy pierwiastki tego wielomianu tworzą ciąg arytmetyczny o różnicy równej 3. Oblicz współczynniki
. Trzy pierwiastki tego wielomianu tworzą ciąg arytmetyczny o różnicy równej 3. Oblicz współczynniki 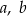 i
i  . Rozważ wszystkie możliwe przypadki.
. Rozważ wszystkie możliwe przypadki.
Odcinek 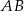 o długości 20 jest zawarty w prostej o równaniu
o długości 20 jest zawarty w prostej o równaniu 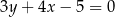 . Symetralna odcinka
. Symetralna odcinka 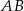 przecina oś
przecina oś 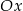 w punkcie
w punkcie 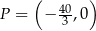 . Oblicz współrzędne końców odcinka
. Oblicz współrzędne końców odcinka 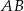 .
.
Funkcja 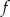 jest określona wzorem
jest określona wzorem 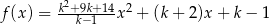 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz całkowite wartości parametru
. Wyznacz całkowite wartości parametru 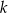 , dla których funkcja
, dla których funkcja 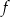 przyjmuje wartość największą i ma dwa różne miejsca zerowe o jednakowych znakach.
przyjmuje wartość największą i ma dwa różne miejsca zerowe o jednakowych znakach.
Podstawą prostopadłościanu jest prostokąt, w którym jeden bok jest dwa razy dłuższy od drugiego. Pole powierzchni całkowitej tego prostopadłościanu jest równe 1. Jakie powinny być wymiary tego prostopadłościanu, aby jego objętość była największa? Oblicz tę największą objętość.

