/Szkoła średnia/Zadania maturalne/Matura 2021/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom rozszerzony 27 lutego 2021 Czas pracy: 180 minut
Zadania zamknięte
Liczba 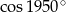 jest równa
jest równa
A) 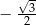 B)
B) 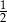 C)
C) 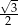 D)
D) 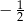
Jacek wykonał rzut trzema sześciennymi kostkami do gry i otrzymał sumę oczek mniejszą niż 5. Prawdopodobieństwo, że Jacek wyrzucił przynajmniej jedną dwójkę jest równe
A) 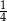 B)
B)  C)
C)  D)
D) 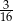
Granica jednostronna 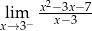
A) jest liczbą rzeczywistą B) jest równa 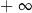 C) nie istnieje D) jest równa
C) nie istnieje D) jest równa 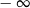
Po przekształceniu wyrażenia algebraicznego 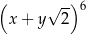 do postaci
do postaci
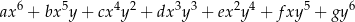
współczynnik 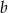 jest równy
jest równy
A) 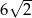 B) 6 C)
B) 6 C) 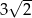 D) 12
D) 12
Zadania otwarte
Funkcja 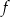 jest określona wzorem
jest określona wzorem 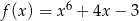 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równanie prostej stycznej do wykresu funkcji
. Wyznacz równanie prostej stycznej do wykresu funkcji 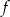 , która jest równoległa do prostej
, która jest równoległa do prostej 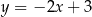 .
.
Przez wierzchołek kąta prostego trójkąta prostokątnego o przyprostokątnych 8 i 15 poprowadzono prostą, która dzieli ten trójkąt na dwa trójkąty o równych obwodach. Znajdź stosunek promieni okręgów wpisanych w otrzymane z podziału trójkąty.
W kwadrat o boku  wpisujemy okrąg. W ten okrąg wpisujemy kwadrat, w który wpisujemy okrąg itd. W ten sposób powstanie nieskończony ciąg kwadratów. Oblicz sumę obwodów wszystkich tych kwadratów.
wpisujemy okrąg. W ten okrąg wpisujemy kwadrat, w który wpisujemy okrąg itd. W ten sposób powstanie nieskończony ciąg kwadratów. Oblicz sumę obwodów wszystkich tych kwadratów.
Liczby dodatnie  i
i 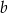 spełniają równość
spełniają równość 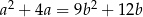 . Wykaż, że
. Wykaż, że 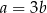 .
.
Rozwiąż równanie ![[ ( π-) ( π)] 1 (sin x)⋅ co s x − 3 + cos x+ 3 = 2 co sx](https://img.zadania.info/zes/0081004/HzesT27x.gif) .
.
Z urny zawierającej 7 kul białych i 3 kule czarne wylosowano bez zwracania 4 kule. Jakie jest prawdopodobieństwo tego, że stosunek liczby kul czarnych do liczby kul białych w urnie uległ zwiększeniu?
W prostokącie 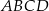 , w którym
, w którym 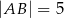 ,
, 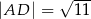 , na przekątnej
, na przekątnej 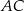 wybrano taki punkt
wybrano taki punkt 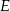 , że
, że 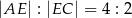 . Oblicz sinus kąta
. Oblicz sinus kąta 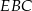 .
.
Okrąg jest styczny do osi układu współrzędnych w punktach 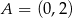 i
i 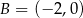 oraz jest styczny do prostej
oraz jest styczny do prostej 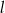 w punkcie
w punkcie 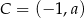 , gdzie
, gdzie 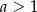 . Wyznacz równanie prostej
. Wyznacz równanie prostej 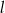 .
.
W graniastosłupie prawidłowym trójkątnym poprowadzono płaszczyznę 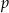 wyznaczoną przez wysokość dolnej podstawy i ten z wierzchołków górnej podstawy, że płaszczyzna
wyznaczoną przez wysokość dolnej podstawy i ten z wierzchołków górnej podstawy, że płaszczyzna  z płaszczyzną podstawy graniastosłupa tworzy kąt ostry
z płaszczyzną podstawy graniastosłupa tworzy kąt ostry  taki, że
taki, że 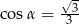 . Pole przekroju graniastosłupa wyznaczonego przez płaszczyznę
. Pole przekroju graniastosłupa wyznaczonego przez płaszczyznę 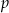 jest równe
jest równe 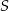 . Oblicz objętość graniastosłupa.
. Oblicz objętość graniastosłupa.
Wyznacz wszystkie wartości parametru 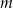 , dla których równanie
, dla których równanie 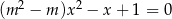 ma dwa różne rozwiązania rzeczywiste
ma dwa różne rozwiązania rzeczywiste 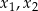 takie, że
takie, że 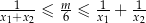 .
.
Betonowy kanał wodny ma mieć przekrój w kształcie trapezu równoramiennego, którego krótsza podstawa i ramiona mają długość po 2 m. Oblicz, jaką długość powinna mieć dłuższa podstawa tego trapezu, aby przez kanał mogło przepłynąć jak najwięcej wody, czyli aby pole powierzchni przekroju kanału było największe. Oblicz to pole przekroju.