/Szkoła średnia/Zadania maturalne/Matura 2022
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom rozszerzony 5 marca 2022 Czas pracy: 180 minut
Zadania zamknięte
Wartość wyrażenia 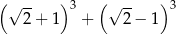 jest równa
jest równa
A) 14 B) 7 C) 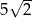 D)
D) 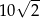
Niech 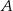 i
i 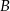 będą takim zdarzeniami losowymi, że
będą takim zdarzeniami losowymi, że 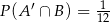 i
i 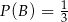 . Wtedy prawdopodobieństwo warunkowe
. Wtedy prawdopodobieństwo warunkowe 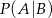 jest równe
jest równe
A) 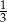 B)
B) 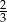 C)
C) 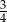 D)
D) 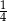
Liczba 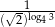 jest równa
jest równa
A) 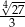 B)
B) 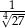 C)
C) 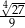 D)
D) 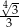
Liczba różnych pierwiastków równania 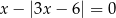 jest równa
jest równa
A) 0 B) 1 C) 2 D) 3
Zadania otwarte
Wynikiem dzielenia wielomianu 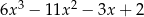 przez dwumian
przez dwumian 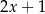 jest trójmian kwadratowy postaci
jest trójmian kwadratowy postaci 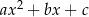 . Oblicz
. Oblicz 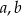 i
i  .
.
Oblicz granicę jednostronną funkcji 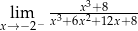 .
.
Oblicz pole trójkąta ograniczonego osiami układu współrzędnych i styczną do paraboli 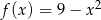 w punkcie
w punkcie 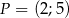 .
.
Kąt ostry rombu 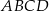 ma miarę
ma miarę 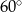 . Na bokach
. Na bokach 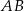 i
i 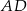 tego rombu wybrano punkty – odpowiednio –
tego rombu wybrano punkty – odpowiednio – 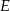 i
i 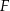 takie, że
takie, że 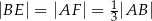 . Odcinki
. Odcinki 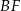 i
i 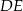 przecinają się w punkcie
przecinają się w punkcie 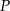 (zobacz rysunek).
(zobacz rysunek).
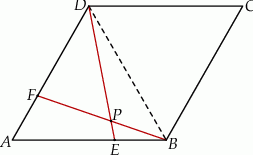
Wykaż, że punkt 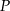 leży na okręgu opisanym na trójkącie
leży na okręgu opisanym na trójkącie 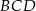 .
.
W trójkąt równoboczny o boku długości 3 wpisano koło, w które następnie wpisano trójkąt równoboczny, a w ten trójkąt znów koło i tak dalej. Oblicz sumę pól wszystkich wpisanych kół.
Pięć ponumerowanych kul rozmieszczamy losowo w czterech ponumerowanych szufladach. Oblicz ile jest możliwości takiego rozmieszczenia kul, aby dokładnie dwie szuflady były puste.
Długości boków trójkąta są w stosunku 2 : 3 : 4. Oblicz wartość wyrażenia
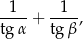
gdzie  oznacza największy, a
oznacza największy, a 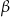 najmniejszy kąt tego trójkąta.
najmniejszy kąt tego trójkąta.
Rozwiąż równanie 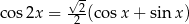 w przedziale
w przedziale 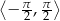 .
.
Punkt 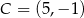 jest wierzchołkiem trójkąta prostokątnego
jest wierzchołkiem trójkąta prostokątnego 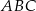 , w którym
, w którym 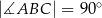 i
i 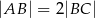 . Prosta
. Prosta 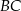 ma równanie
ma równanie 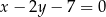 , a punkt
, a punkt 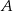 leży na prostej
leży na prostej 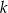 o równaniu
o równaniu 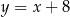 . Wyznacz współrzędne środka okręgu opisanego na trójkącie
. Wyznacz współrzędne środka okręgu opisanego na trójkącie 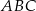 .
.
Wyznacz wszystkie wartości parametru 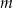 , dla których równanie
, dla których równanie
![2 2 (x+ 2)[x − (m + 1)x − 6m + 3m )] = 0](https://img.zadania.info/zes/0075148/HzesT55x.gif)
ma dokładnie dwa rozwiązania.
Suma długości trzech krawędzi prostopadłościanu wychodzących z jednego wierzchołka jest równa 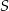 . Długość jednej z tych krawędzi jest dwa razy większa od drugiej. Oblicz promień sfery opisanej na tym z rozważanych prostopadłościanów, którego objętość jest największa.
. Długość jednej z tych krawędzi jest dwa razy większa od drugiej. Oblicz promień sfery opisanej na tym z rozważanych prostopadłościanów, którego objętość jest największa.

