Zadanie nr 8177681
Narysuj wykres funkcji 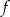 określonej wzorem
określonej wzorem 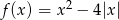 i na jego podstawie wyznacz liczbę rozwiązań równania
i na jego podstawie wyznacz liczbę rozwiązań równania 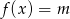 w zależności od wartości parametru
w zależności od wartości parametru 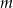 .
.
Rozwiązanie
Wzór danej funkcji możemy zapisać w postaci
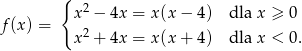
Zatem jej wykresem są dwa kawałki parabol: na prawo od osi 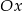 parabola
parabola 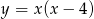 , a na lewo parabola
, a na lewo parabola 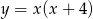 . Teraz bez problemy szkicujemy wykres funkcji
. Teraz bez problemy szkicujemy wykres funkcji 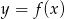 .
.
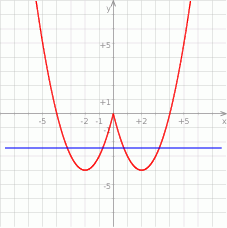
Z obrazka odczytujemy liczbę punktów wspólnych wykresu z prostą 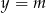 .
.
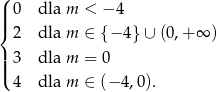
Odpowiedź: