/Szkoła średnia/Zadania maturalne/Matura 2022/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom rozszerzony 12 marca 2022 Czas pracy: 180 minut
Zadania zamknięte
Różnica 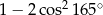 jest równa
jest równa
A) 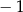 B)
B) 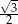 C)
C) 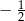 D)
D) 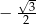
Reszta z dzielenia wielomianu 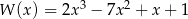 przez dwumian
przez dwumian 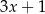 jest równa
jest równa
A) 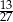 B)
B) 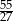 C)
C) 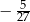 D)
D) 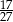
Wektory ![→a = [m − 3,m + 3]](https://img.zadania.info/zes/0075560/HzesT11x.gif) oraz
oraz ![→ b = [m1,5,3]](https://img.zadania.info/zes/0075560/HzesT12x.gif) mają równe długości wtedy i tylko wtedy, gdy
mają równe długości wtedy i tylko wtedy, gdy
A) 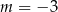 lub
lub 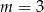 B)
B) 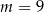 lub
lub 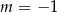 C)
C) 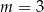 D)
D) 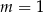 lub
lub 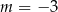
Dany jest nieskończony ciąg geometryczny, w którym suma wszystkich wyrazów jest 5 razy większa od sumy wszystkich wyrazów o numerach parzystych. Iloraz tego ciągu jest równy
A) 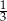 B)
B)  C)
C) 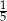 D)
D) 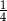
Zadania otwarte
Oblicz granicę 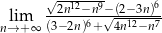 .
.
Niech 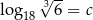 . Wykaż, że
. Wykaż, że 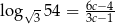 .
.
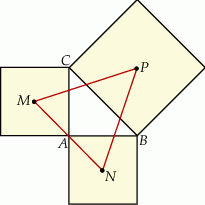
Na zewnątrz równoramiennego trójkąta prostokątnego 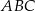 zbudowano kwadraty tak, że bok każdego kwadratu jest jednocześnie bokiem trójkąta. Środki symetrii tych kwadratów połączono odcinkami i otrzymano trójkąt
zbudowano kwadraty tak, że bok każdego kwadratu jest jednocześnie bokiem trójkąta. Środki symetrii tych kwadratów połączono odcinkami i otrzymano trójkąt 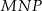 . Wykaż, że pole trójkąta
. Wykaż, że pole trójkąta 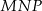 jest dwa razy większe od pola trójkąta
jest dwa razy większe od pola trójkąta 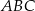 .
.
Wyznacz maksymalne przedziały monotoniczności funkcji 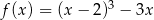 .
.
Ze zbioru wszystkich liczb naturalnych czterocyfrowych losujemy jedną liczbę. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że wylosowana liczba jest podzielna przez 18, jeśli wiadomo, że jest ona podzielna przez 24.
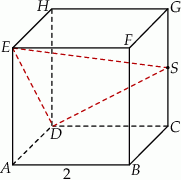
Dany jest sześcian 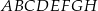 o krawędzi długości 2. Punkt
o krawędzi długości 2. Punkt 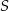 jest środkiem krawędzi
jest środkiem krawędzi 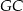 (zobacz rysunek). Oblicz promień okręgu opisanego na trójkącie
(zobacz rysunek). Oblicz promień okręgu opisanego na trójkącie 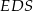 .
.
Wyznacz wszystkie rozwiązania równania 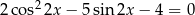 należące do przedziału
należące do przedziału 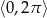 .
.
Wyznacz równania prostych stycznych do okręgu o równaniu 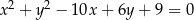 równoległych do prostej o równaniu
równoległych do prostej o równaniu 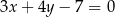 .
.
Wysokość 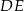 rombu
rombu 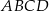 dzieli bok
dzieli bok 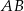 tego rombu tak, że
tego rombu tak, że 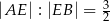 (zobacz rysunek).
(zobacz rysunek).
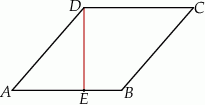
Oblicz wartość wyrażenia
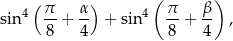
gdzie  i
i 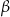 są dwoma sąsiednimi kątami wewnętrznymi rombu
są dwoma sąsiednimi kątami wewnętrznymi rombu 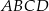 .
.
Wyznacz wszystkie wartości parametru 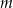 , dla których funkcja kwadratowa
, dla których funkcja kwadratowa 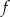 określona wzorem
określona wzorem
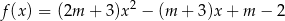
ma dwa różne pierwiastki rzeczywiste 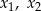 spełniające warunek
spełniające warunek 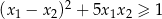 .
.
Dana jest funkcja 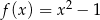 określona dla
określona dla 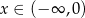 . W jakim punkcie wykresu tej funkcji należy poprowadzić styczną tak, aby trójkąt ograniczony tą styczną i osiami układu współrzędnych miał najmniejsze pole? Oblicz to pole.
. W jakim punkcie wykresu tej funkcji należy poprowadzić styczną tak, aby trójkąt ograniczony tą styczną i osiami układu współrzędnych miał najmniejsze pole? Oblicz to pole.

