/Szkoła podstawowa/Egzamin ósmoklasisty/Egzamin 2022/Egzamin
Egzamin Ósmoklasisty
z Matematyki (termin dodatkowy) 14 czerwca 2022 Czas pracy: 100 minut
Wśród pewnej grupy osób przeprowadzono ankietę. Jedno z pytań brzmiało: Jaka jest twoja ulubiona pora roku?. Każdy ankietowany wskazał tylko jedną porę roku. Rozkład udzielonych odpowiedzi na to pytanie przedstawiono na diagramie.
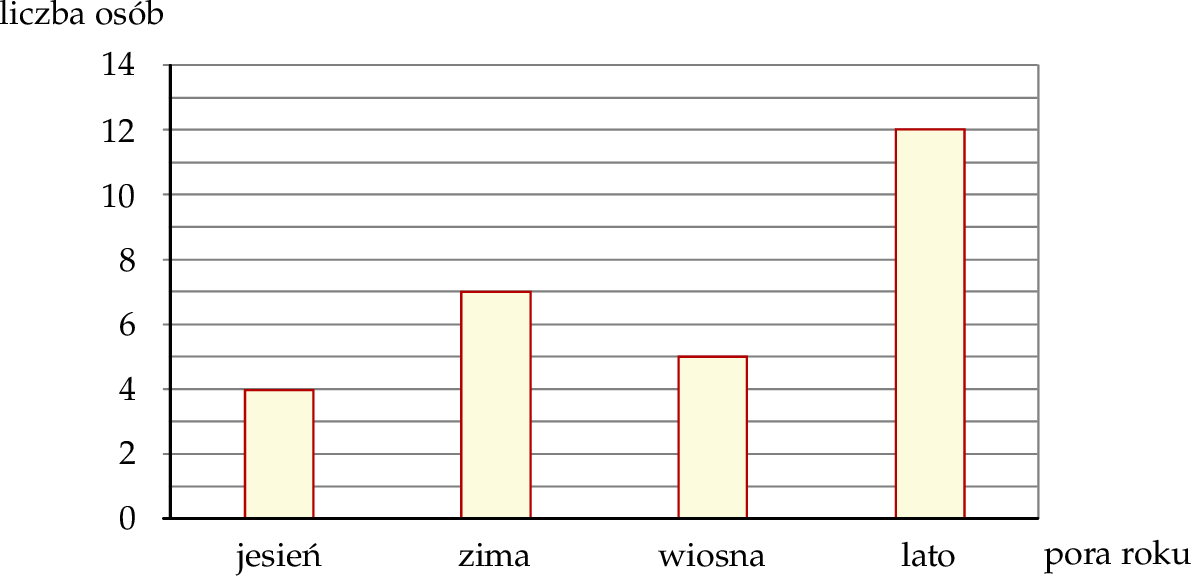
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Zima jest ulubioną porą roku dla mniej niż 24% liczby osób ankietowanych. | P | F |
Lato jest ulubioną porą roku dla  liczby osób ankietowanych. liczby osób ankietowanych. | P | F |
Córka obecnie jest 4 razy młodsza od swojej mamy. Razem mają 60 lat. Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Mama obecnie ma A/B lat.
A) 48 B) 45
Córka za 8 lat będzie miała C/D .
C) 23 lata D) 20 lat
Liczby:  ,
, 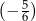 ,
, 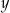 , są uporządkowane rosnąco. Liczba
, są uporządkowane rosnąco. Liczba 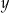 jest o 0,5 większa od
jest o 0,5 większa od 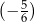 , a liczba
, a liczba 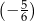 jest o 0,5 większa od liczby
jest o 0,5 większa od liczby  . Jakie wartości mają liczby
. Jakie wartości mają liczby  i
i 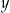 ?
?
A) 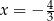 i
i 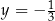 B)
B) 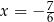 i
i 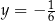
C) 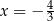 i
i 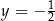 D)
D) 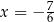 i
i 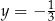
Rozwiązaniem równania 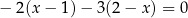 jest liczba
jest liczba
A) 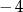 B)
B) 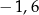 C) 0,8 D) 4 E) 8
C) 0,8 D) 4 E) 8
O godzinie 14:50 Maciek wyruszył w podróż pociągiem z Gdańska do Grudziądza. Najpierw dojechał do Iławy, gdzie po 50–minutowym oczekiwaniu wsiadł do pociągu, którym dojechał do Grudziądza. Na rysunku pokazano, jak w czasie przebiegała podróż Maćka. Na osi czas przejazdu z Gdańska do Grudziądza podzielono na 20 jednakowych odstępów.
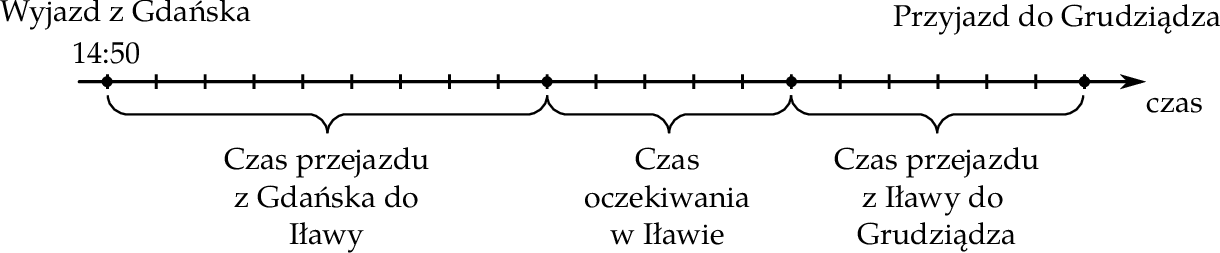
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Przejazd z Iławy do Grudziądza trwał jedną godzinę. | P | F |
| Maciek przyjechał do Grudziądza o godzinie 18:10. | P | F |
Dane są trzy liczby:
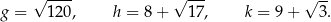
Które spośród tych liczb są mniejsze od liczby 11?
A) Tylko 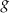 . B) Tylko
. B) Tylko 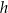 i
i 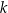 . C) Tylko
. C) Tylko 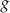 i
i 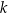 . D) Tylko
. D) Tylko 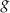 i
i 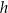 .
.
Liczbę 404 można zapisać w postaci 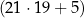 .
.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Resztą z dzielenia liczby 404 przez 19 jest 5. | P | F |
| Jeśli liczbę 404 zmniejszymy o 5, to otrzymamy liczbę podzielną przez 21. | P | F |
Na tablicy zapisano wszystkie różne liczby dwucyfrowe, które jednocześnie spełniają trzy warunki: są mniejsze od 40, są podzielne przez 3, suma cyfr każdej z nich jest większa od 7. Ile liczb zapisano na tablicy?
A) 3 B) 4 C) 5 D) 6
Biuro podróży w ramach oferty promocyjnej obniżyło cenę wycieczki o 20%. Pani Anna skorzystała z promocji i za wycieczkę zapłaciła 1500 zł. Jaka była cena wycieczki przed obniżką?
A) 1800 zł. B) 1875 zł. C) 2000 zł. D) 2175 zł.
Liczba 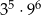 jest równa
jest równa
A) 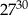 B)
B) 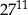 C)
C) 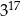 D)
D) 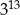
Dany jest wzór na pole powierzchni całkowitej graniastosłupa:
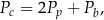
gdzie: 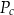 – pole powierzchni całkowitej,
– pole powierzchni całkowitej,  – pole podstawy,
– pole podstawy, 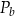 – pole powierzchni bocznej. Pole podstawy
– pole powierzchni bocznej. Pole podstawy 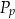 wyznaczone poprawnie z powyższego wzoru opisano równaniem
wyznaczone poprawnie z powyższego wzoru opisano równaniem
A) 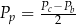 B)
B) 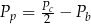 C)
C) 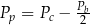 D)
D) 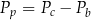
Na rysunku przedstawiono prostokąt i dwa trójkąty równoramienne 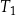 i
i 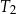 oraz podano długości ich boków.
oraz podano długości ich boków.
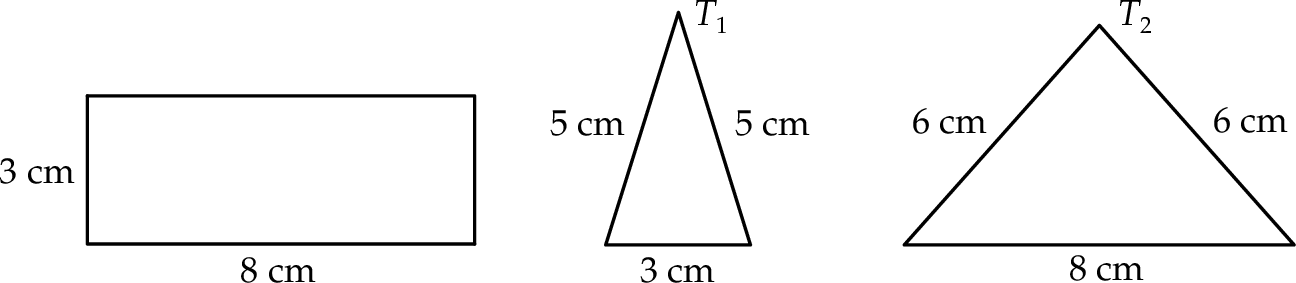
Czy te trzy wielokąty mogą być ścianami jednego ostrosłupa? Wybierz odpowiedź T lub N i jej uzasadnienie spośród zdań A–C.
| Tak | Nie |
| ponieważ | |
| A) | długości boków prostokąta są równe długościom podstaw trójkątów 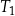 i i 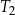 . . |
| B) | trójkąty 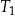 i i 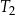 mają podstawy różnej długości. mają podstawy różnej długości. |
| C) | ramiona trójkąta 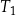 mają inną długość niż ramiona trójkąta mają inną długość niż ramiona trójkąta 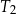 . . |
W pewnym rombie jeden z kątów wewnętrznych ma miarę 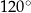 . Obwód tego rombu jest równy 24 cm. Dłuższa przekątna tego rombu ma długość
. Obwód tego rombu jest równy 24 cm. Dłuższa przekątna tego rombu ma długość
A) 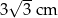 B) 6 cm C)
B) 6 cm C) 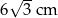 D) 12 cm
D) 12 cm
Na rysunku przedstawiono prostokąt. Długość dłuższego boku oznaczono symbolem  oraz opisano za pomocą wyrażenia algebraicznego
oraz opisano za pomocą wyrażenia algebraicznego  . Długość krótszego boku oznaczono symbolem
. Długość krótszego boku oznaczono symbolem 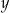 oraz opisano za pomocą wyrażenia algebraicznego
oraz opisano za pomocą wyrażenia algebraicznego 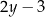 .
.
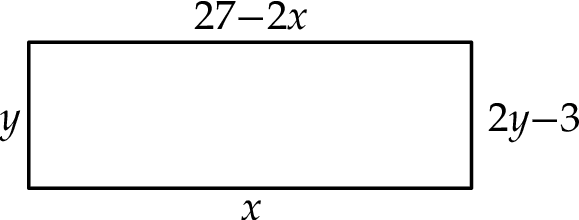
Które równanie nie opisuje poprawnej zależności między wartościami  i
i 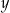 ?
?
A) 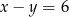 B)
B) 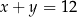 C)
C) 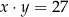 D)
D) 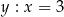
Uzupełnij zdania. Wybierz odpowiedź spośród oznaczonych literami A i B oraz odpowiedź spośród oznaczonych literami C i D.
Wartość wyrażenia 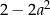 dla
dla 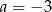 jest równa A/B .
jest równa A/B .
A) 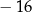 B) 20
B) 20
1 Wyrażenie 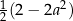 można przekształcić do postaci C/D .
można przekształcić do postaci C/D .
C) 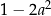 D)
D) 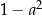
W kasie są banknoty 20–złotowe i 50–złotowe. Liczba banknotów 20–złotowych jest taka sama jak liczba banknotów 50–złotowych. Łączna wartość wszystkich banknotów 50–złotowych jest o 6 tysięcy złotych większa od łącznej wartości wszystkich banknotów 20–złotowych. Oblicz, ile banknotów 20–złotowych jest w kasie.
Janek miał łącznie 84 piłeczki, z których każda była w jednym z trzech kolorów: czerwonym, zielonym lub niebieskim. Liczby piłeczek czerwonych, zielonych i niebieskich są – odpowiednio – kolejnymi liczbami podzielnymi przez 7. Janek rozdzielił wszystkie piłeczki na siedem identycznych zestawów, przy czym w każdym z nich znalazły się piłeczki w trzech kolorach. Oblicz, ile piłeczek czerwonych, ile – zielonych, a ile – niebieskich było w jednym zestawie.
Prostokątna łąka jest podzielona na dwie części 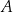 i
i  , tak jak pokazano na rysunku. Każda z tych części ma kształt trapezu.
, tak jak pokazano na rysunku. Każda z tych części ma kształt trapezu.
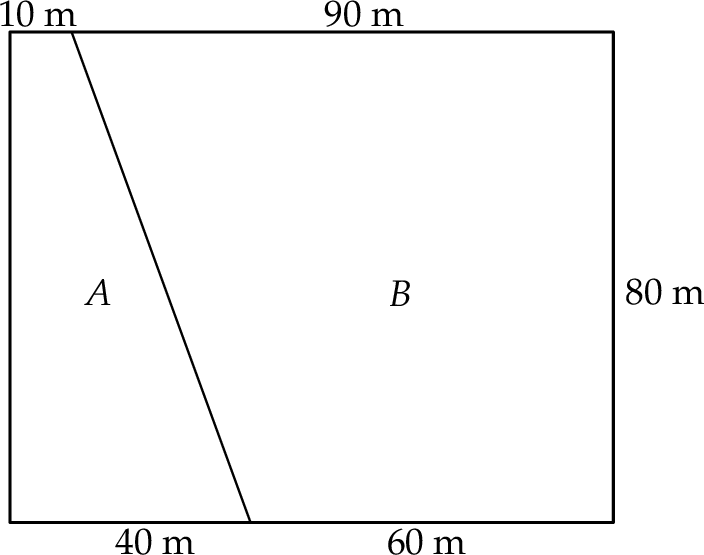
Kosiarka w ciągu każdej godziny swojej pracy kosi trawę z powierzchni o takim samym polu. Trawę z części  kosiarka skosiła w ciągu trzech godzin. Oblicz, ile godzin kosiarka będzie kosiła trawę w części
kosiarka skosiła w ciągu trzech godzin. Oblicz, ile godzin kosiarka będzie kosiła trawę w części  .
.
Na rysunku przedstawiono graniastosłup prosty, którego podstawą jest trójkąt prostokątny. Długość jednej z przyprostokątnych jest równa 8 cm, a długość przeciwprostokątnej jest równa 10 cm. Najmniejsza ściana boczna tego graniastosłupa ma pole równe 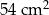 .
.

Oblicz sumę długości wszystkich krawędzi tego graniastosłupa.

