/Szkoła średnia/Geometria/Geometria analityczna/Równanie prostej/Symetralna

Zadanie nr 3605171

Dany jest punkt 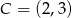C = (2,3) i prosta o równaniu 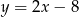y = 2x − 8 będąca symetralną odcinka 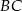BC . Wyznacz współrzędne punktu 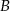B . Wykonaj obliczenia uzasadniające odpowiedź.

Wersja PDF

Rozwiązanie

Zacznijmy od schematycznego rysunku.

PIC

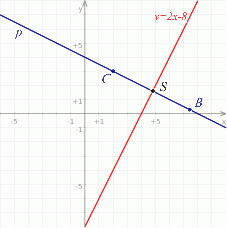
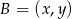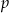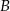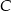Aby wyznaczyć szukany punkt B = (x,y) , znajdziemy najpierw równanie prostej p zawierającej punkty B i C . Później wyznaczymy punkt 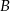B , korzystając z faktu, że punkt przecięcia 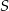S tych dwóch prostych jest środkiem odcinka BC .

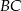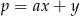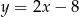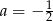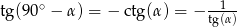Prosta p = ax + y jest prostopadła do prostej y = 2x − 8 zatem jej współczynnik kierunkowy a spełnia warunek a = − 12 (ponieważ współczynnik kierunkowy prostej to tangens kąta jaki tworzy ona z osią x , to ostatnia równość wynika np. ze wzoru: tg(90∘ − α ) = − ctg(α) = − -1-- tg(α) ). Aby wyznaczyć 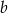b korzystamy z faktu, że prosta ta przechodzi przez punkt C = (2,3) :

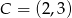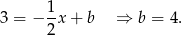
3 = − 1x + b ⇒ b = 4. 2

Wyznaczmy teraz współrzędne punktu 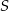S :

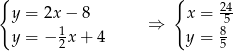
{ { 24 y = 2x − 8 ⇒ x = -5 y = − 1x + 4 y = 8 2 5

Ponieważ 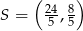( ) 24 8 S = 5 , 5 jest środkiem odcinka 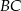BC , to współrzędne punktu 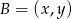B = (x,y) spełniają:

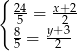
{ 245-= x+22- 8 y+3- 5 = 2

Po rozwiązaniu tego układu równań otrzymujemy 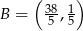( 38 1) B = 5-,5 .  
Odpowiedź: (38 1) B = 5 , 5

Wersja PDF