/Szkoła średnia/Zadania maturalne/Matura 2023
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom podstawowy 18 marca 2023 Czas pracy: 180 minut
Liczbę 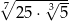 można zapisać w postaci
można zapisać w postaci
A) 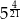 B)
B) 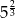 C)
C) 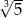 D)
D) 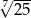
Do 1,6 kg roztworu soli dolano 0,9 litra wody i stężenie procentowe roztworu zmniejszyło się o 4,5 punktu procentowego. Jakie jest stężenie procentowe otrzymanego roztworu?
A) 8% B) 5% C) 9% D) 6%
Wszystkich liczb naturalnych trzycyfrowych, w których zapisie dziesiętnym występuje przynajmniej jedna cyfra 2, jest
A) 648 B) 171 C) 252 D) 351
Liczby rzeczywiste  i
i 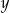 są dodatnie oraz
są dodatnie oraz 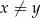 . Wyrażenie
. Wyrażenie 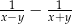 można przekształcić do postaci
można przekształcić do postaci
A) 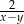 B)
B) 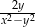 C)
C) 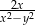 D)
D) 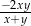
Na rysunku zaznaczono niektóre z kątów utworzonych przez prostą 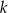 i dwie równoległe do siebie proste
i dwie równoległe do siebie proste 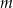 i
i  . (zobacz rysunek).
. (zobacz rysunek).
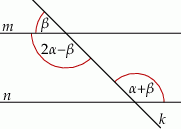
Dokończ zdanie. Wybierz dwie odpowiedzi, tak aby dla każdej z nich dokończenie poniższego zdania było prawdziwe.
Układem równań, w którym zapisano prawidłowe zależności między miarami kątów utworzonych przez te proste, jest układ
A) 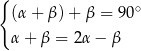 B)
B) 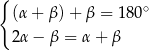 C)
C) 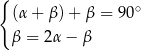
D) 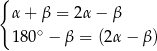 E)
E) 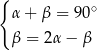 F)
F) 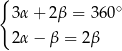
Funkcja 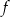 jest określona wzorem
jest określona wzorem 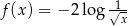 dla wszystkich liczb rzeczywistych dodatnich
dla wszystkich liczb rzeczywistych dodatnich  . Funkcja
. Funkcja 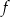 przyjmuje wartość równą
przyjmuje wartość równą 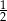 dla argumentu
dla argumentu  równego
równego
A) 100 B) 0,01 C) 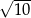 D) 1 000
D) 1 000
Dla jakiej całkowitej wartości liczby  spełniona jest nierówność
spełniona jest nierówność 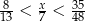 ?
?
A) 4 B) 3 C) 2 D) 5
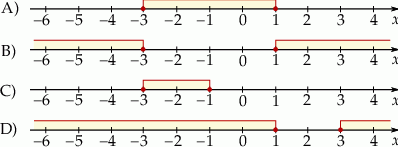
Spośród rysunków A–D wybierz ten, na którym prawidłowo zaznaczono na osi liczbowej zbiór wszystkich liczb rzeczywistych spełniających nierówność
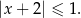
Wykaż, że dla każdej liczby naturalnej  liczba
liczba  jest podzielna przez 14.
jest podzielna przez 14.
Równanie
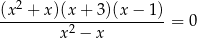
ma w zbiorze liczb rzeczywistych dokładnie
A) jedno rozwiązanie: 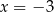
B) dwa rozwiązania: 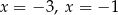
C) trzy rozwiązania: 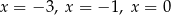
D) cztery rozwiązania: 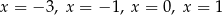
Która z poniższych równości jest prawdziwa dla każdej liczby rzeczywistej  ?
?
A) 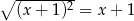 B)
B) 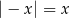 C)
C) 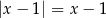 D)
D) 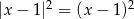
Ze zbioru 26 liter alfabetu łacińskiego  losujemy bez zwracania trzy razy jedną literę. Oblicz prawdopodobieństwo tego, że wśród wylosowanych liter znalazła się przynajmniej jedna z liter
losujemy bez zwracania trzy razy jedną literę. Oblicz prawdopodobieństwo tego, że wśród wylosowanych liter znalazła się przynajmniej jedna z liter 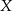 ,
, 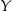 lub
lub 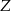 .
.
Dana jest nierówność
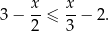
Najmniejszą liczbą całkowitą, która spełnia tę nierówność, jest
A) 6 B) 5 C) 7 D) 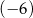
Informacja do zadań 14.1 i 14.2
Dany jest trójkąt równoboczny 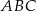 o boku długości 8. Ze środka
o boku długości 8. Ze środka 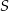 boku
boku 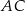 zakreślono koło o promieniu równym połowie boku trójkąta (zobacz rysunek).
zakreślono koło o promieniu równym połowie boku trójkąta (zobacz rysunek).
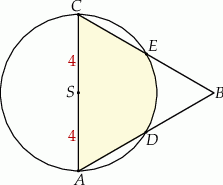
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Krótsze z łuków wyciętych przez punkty  i i  , oraz , oraz  i i 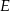 z danego okręgu, mają tą samą długość. z danego okręgu, mają tą samą długość. | P | F |
Odcinek 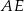 jest dwa razy dłuższy od odcinka jest dwa razy dłuższy od odcinka 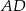 . . | P | F |
Pole powierzchni części wspólnej koła i trójkąta jest równe
A) 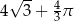 B)
B) 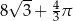 C)
C) 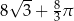 D)
D) 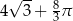
Wysokość ostrosłupa prawidłowego czworokątnego jest równa 8. Krawędź boczna jest nachylona do płaszczyzny podstawy pod kątem  takim, że
takim, że 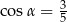 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Klient banku wypłacił z okienka kasowego kwotę 4010 zł. Pracownik banku wydał kwotę w banknotach o nominałach 20 zł, 50 zł oraz 100 zł. Banknotów 100–złotowych było trzy razy więcej niż 50–złotowych, a banknotów 20–złotowych było o 3 mniej niż 50–złotowych. Ile banknotów 20–złotowych otrzymał klient?
A) 12 B) 6 C) 8 D) 11
Dany jest ciąg 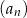 określony wzorem
określony wzorem 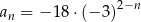 dla każdej liczby naturalnej
dla każdej liczby naturalnej 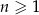 . Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Suma trzech początkowych wyrazów ciągu 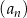 jest równa 42. jest równa 42. | P | F |
Ciąg 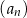 jest ciągiem geometrycznym o ilorazie równym jest ciągiem geometrycznym o ilorazie równym 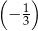 . . | P | F |
Punkty 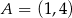 i
i 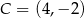 wyznaczają przekątną kwadratu
wyznaczają przekątną kwadratu 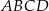 . Pole tego kwadratu jest równe
. Pole tego kwadratu jest równe
A) 45 B) 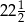 C) 18 D)
C) 18 D) 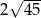
Dany jest ciąg 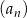 określony wzorem
określony wzorem 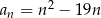 dla każdej liczby naturalnej
dla każdej liczby naturalnej 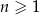 . Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
. Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Szesnasty wyraz ciągu 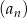 jest większy od wyrazu piętnastego. jest większy od wyrazu piętnastego. | P | F |
Ciąg 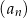 jest rosnący. jest rosnący. | P | F |
Dany jest równoległobok 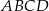 , w którym
, w którym 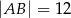 ,
, 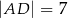 oraz
oraz
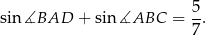
Oblicz pole równoległoboku 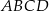 .
.
W kartezjańskim układzie współrzędnych 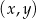 dane są: punkt
dane są: punkt 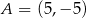 oraz okrąg o równaniu
oraz okrąg o równaniu 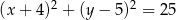 . Odległość punktu
. Odległość punktu 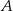 od środka tego okręgu jest równa
od środka tego okręgu jest równa
A) 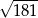 B) 3 C)
B) 3 C) 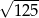 D)
D) 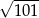
Bok 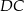 prostokąta
prostokąta 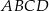 jest zawarty w prostej o równaniu
jest zawarty w prostej o równaniu 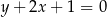 . Jedna z przekątnych tego prostokąta może być zawarta w prostej o równaniu
. Jedna z przekątnych tego prostokąta może być zawarta w prostej o równaniu
A) 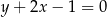 B)
B) 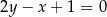 C)
C) 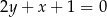 D)
D) 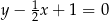
Prosta 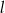 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 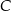 . Jeżeli kąt
. Jeżeli kąt 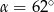 , to miara kąta
, to miara kąta 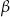 jest równa
jest równa
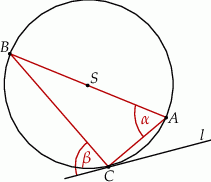
A) 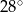 B)
B) 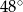 C)
C) 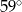 D)
D) 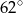
Dane są punkty 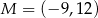 ,
, 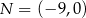 oraz
oraz 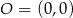 . Tangens kąta ostrego
. Tangens kąta ostrego 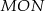 jest równy
jest równy
A) 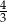 B)
B) 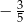 C)
C) 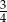 D)
D) 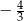
W pojemniku są wyłącznie kule białe, czerwone, niebieskie i żółte. Kul białych jest tyle samo co kul niebieskich, kul czerwonych jest dwa razy więcej niż kul żółtych, a stosunek liczby kul żółtych do liczby kul niebieskich jest równy 4 : 5. Z pojemnika losujemy jedną kulę. Prawdopodobieństwo wylosowania kuli, która nie jest czerwona jest równe
A) 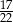 B)
B)  C)
C) 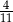 D)
D) 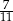
Dana jest funkcja kwadratowa 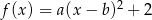 , gdzie
, gdzie 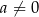 i
i 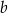 są liczbami rzeczywistymi. Funkcja
są liczbami rzeczywistymi. Funkcja 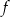 nie przyjmuje wartości większych od 2.
nie przyjmuje wartości większych od 2.
Dokończ zdanie tak, aby było prawdziwe. Wybierz odpowiedź A albo B oraz jej uzasadnienie 1, 2 albo 3.
Funkcja 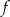
| A) ma miejsca zerowe, | B) nie ma miejsc zerowych, |
| ponieważ | |
| 1) | 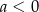 i i 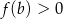 . . |
| 2) | 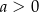 i i 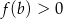 . . |
| 3) | 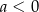 i i 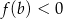 . . |
Na płaszczyźnie, w kartezjańskim układzie współrzędnych 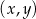 , dane są punkty
, dane są punkty 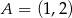 i
i 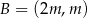 , gdzie
, gdzie 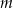 jest liczbą rzeczywistą, oraz prosta
jest liczbą rzeczywistą, oraz prosta 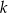 o równaniu
o równaniu 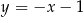 . Prosta przechodząca przez punkty
. Prosta przechodząca przez punkty 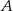 i
i 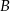 jest prostopadła do prostej
jest prostopadła do prostej 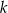 , gdy
, gdy
A) 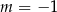 B)
B) 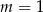 C)
C) 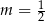 D)
D) 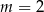
Reszta z dzielenia liczby 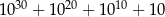 przez 12 jest równa
przez 12 jest równa
A) 8 B) 10 C) 2 D) 4
Podstawą ostrosłupa jest kwadrat  o boku długości 4. Krawędź boczna
o boku długości 4. Krawędź boczna  jest prostopadła do podstawy i ma długość 3 (zobacz rysunek).
jest prostopadła do podstawy i ma długość 3 (zobacz rysunek).
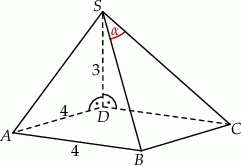
Jeżeli  jest katem pomiędzy krawędziami bocznymi
jest katem pomiędzy krawędziami bocznymi  i
i 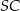 , to
, to
A) 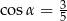 B)
B) 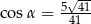 C)
C) 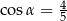 D)
D) 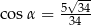
Informacja do zadań 30.1 i 30.2
Basen ma długość 25 m. Przy głębszym z brzegów jego głębokość jest równa 1,8 m. Przekrój podłużny tego basenu przedstawiono poglądowo na rysunku. Głębokość  basenu zmienia się wraz z odległością
basenu zmienia się wraz z odległością  od brzegu w sposób opisany funkcją:
od brzegu w sposób opisany funkcją:
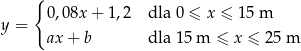
Odległość  jest mierzona od płytszego brzegu w poziomie na powierzchni wody (zobacz rysunek). Wielkości
jest mierzona od płytszego brzegu w poziomie na powierzchni wody (zobacz rysunek). Wielkości  i
i  są wyrażone w metrach.
są wyrażone w metrach.
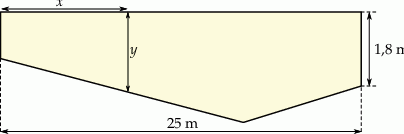
Największa głębokość basenu jest równa
A) 5,4 m B) 3,6 m C) 2,4 m D) 1,8 m
Oblicz wartość współczynnika  oraz wartość współczynnika
oraz wartość współczynnika 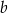 .
.
Rozważamy wszystkie trapezy równoramienne o obwodzie równym 96 i kącie ostrym o mierze  .
.
- Podaj wzór funkcji opisującej zależność pola takiego trapezu od długości
 jego ramienia.
jego ramienia. - Oblicz wymiary tego z rozważanych trapezów, który ma największe pole, i oblicz to największe pole.
Informacja do zadań 32.1 i 32.2
W pewnej grupie 100 uczniów przeprowadzono sondaż dotyczący dziennego czasu korzystania z komputera. Wyniki sondażu przedstawia poniższy diagram. Na osi poziomej podano – wyrażony w godzinach – dzienny czas korzystania przez ucznia z komputera. Na osi pionowej przedstawiono liczbę uczniów, którzy dziennie korzystają z komputera przez określony czas.
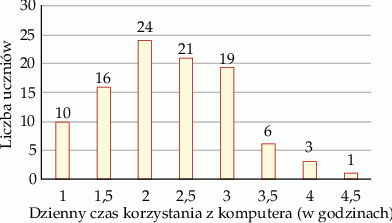
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Mediana dziennego czasu korzystania przez ucznia z komputera jest równa 2 godziny. | P | F |
| Połowa z tej grupy uczniów korzysta dziennie z komputera przez więcej niż 2 godziny. | P | F |
Dominanta dziennego czasu korzystania przez ucznia z komputera jest równa
A) 2,25 godziny B) 2,50 godziny C) 1,5 godziny D) 2 godziny

