/Szkoła średnia/Zadania maturalne/Matura 2023/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom rozszerzony 25 marca 2023 Czas pracy: 180 minut
Oblicz
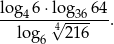
Prostą o równaniu 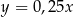 przesunięto o wektor postaci
przesunięto o wektor postaci ![[1 ,m]](https://img.zadania.info/zes/0078420/HzesT2x.gif) w taki sposób, że przesunięta prosta jest styczna do wykresu funkcji
w taki sposób, że przesunięta prosta jest styczna do wykresu funkcji 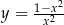 . Oblicz wartość
. Oblicz wartość 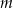 .
.
Oblicz granicę
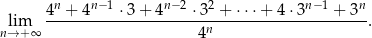
Maszyna napełnia torebki herbatą. Każda torebka ma zostać napełniona 200 g herbaty. Torebkę, która zawiera mniej niż 200 g herbaty, nazywamy torebką z niedowagą. Prawdopodobieństwo tego, że pojedyncza torebka napełniona przez tę maszynę jest z niedowagą, jest równe 0,05. Oblicz, ile torebek herbaty należy poddać kontroli, aby prawdopodobieństwo otrzymania w kontrolowanej partii przynajmniej jednej torebki z niedowagą było większe niż 0,7.
Wykaż, że jeżeli liczby dodatnie 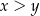 spełniają warunki:
spełniają warunki: 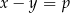 i
i 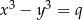 , to
, to
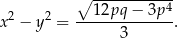
Rozwiąż równanie 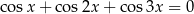 w przedziale
w przedziale ![[0,2π]](https://img.zadania.info/zes/0078420/HzesT11x.gif) .
.
W romb o boku  wpisano dwa okręgi w ten sposób, że okręgi te są styczne zewnętrznie i każdy z nich jest styczny do dwóch sąsiednich boków rombu przecinających się pod kątem ostrym
wpisano dwa okręgi w ten sposób, że okręgi te są styczne zewnętrznie i każdy z nich jest styczny do dwóch sąsiednich boków rombu przecinających się pod kątem ostrym  (zobacz rysunek).
(zobacz rysunek).
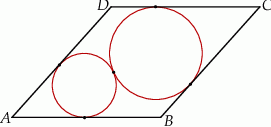
Udowodnij, że suma promieni tych okręgów jest równa 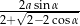 .
.
Informacja do zadań 8.1 i 8.2
Na przedziale ![[− 1,7 ]](https://img.zadania.info/zes/0078420/HzesT16x.gif) określono dwie funkcje:
określono dwie funkcje: 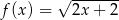 i
i 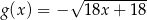 . Rozpatrujemy wszystkie trapezy
. Rozpatrujemy wszystkie trapezy 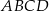 , których wierzchołki
, których wierzchołki 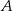 i
i 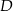 leżą na wykresie funkcji
leżą na wykresie funkcji 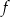 , a wierzchołki
, a wierzchołki 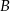 i
i 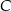 leżą na wykresie funkcji
leżą na wykresie funkcji 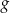 . Podstawy rozpatrywanych trapezów są równoległe do osi
. Podstawy rozpatrywanych trapezów są równoległe do osi 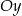 (zobacz rysunek).
(zobacz rysunek).
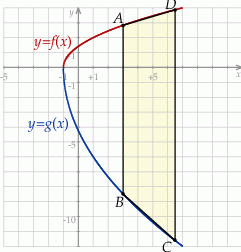
Wykaż, że jeżeli pierwsza współrzędna punktów 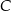 i
i 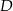 jest równa 7, a druga współrzędna punktu
jest równa 7, a druga współrzędna punktu 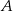 jest równa
jest równa 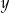 , to pole trapezu
, to pole trapezu 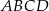 jest równe
jest równe
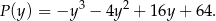
Oblicz współrzędne wierzchołków tego z rozpatrywanych trapezów, w którym 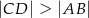 , i który ma największe możliwe pole. Oblicz to największe pole. Przy rozwiązywaniu zadania możesz skorzystać z tego, że jeżeli pierwsza współrzędna wierzchołka
, i który ma największe możliwe pole. Oblicz to największe pole. Przy rozwiązywaniu zadania możesz skorzystać z tego, że jeżeli pierwsza współrzędna wierzchołka 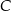 trapezu
trapezu 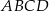 jest równa 7, a druga współrzędna wierzchołka
jest równa 7, a druga współrzędna wierzchołka 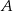 jest równa
jest równa 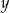 , to pole trapezu wyraża się wzorem
, to pole trapezu wyraża się wzorem
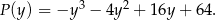
Dany jest ostrosłup prawidłowy trójkątny 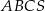 o podstawie
o podstawie 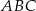 . Krawędź podstawy tego ostrosłupa ma długość
. Krawędź podstawy tego ostrosłupa ma długość  . Ściana boczna jest nachylona do płaszczyzny podstawy pod kątem
. Ściana boczna jest nachylona do płaszczyzny podstawy pod kątem  takim, że
takim, że 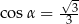 . Przez środek
. Przez środek 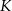 krawędzi
krawędzi 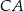 i środek
i środek 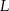 krawędzi
krawędzi 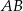 poprowadzono płaszczyznę
poprowadzono płaszczyznę 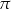 prostopadłą do płaszczyzny
prostopadłą do płaszczyzny 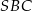 . Oblicz pole otrzymanego przekroju.
. Oblicz pole otrzymanego przekroju.
Dane jest równanie
![2 (x − 2 )⋅[(m − 7)x + 2(m + 3 )x− (2m + 3)] = 0](https://img.zadania.info/zes/0078420/HzesT51x.gif)
z niewiadomą  i parametrem
i parametrem 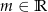 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 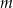 , dla których to równanie ma trzy różne rozwiązania rzeczywiste tego samego znaku.
, dla których to równanie ma trzy różne rozwiązania rzeczywiste tego samego znaku.
Dane są 4 liczby, z których 3 pierwsze tworzą ciąg geometryczny, a 3 ostatnie tworzą ciąg arytmetyczny. Suma pierwszej i czwartej wynosi 22, a suma drugiej i trzeciej wynosi 4. Wyznacz te 4 liczby.
W kartezjańskim układzie współrzędnych dany jest romb 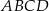 , którego bok
, którego bok 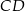 i przekątna
i przekątna 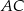 są zawarte w prostych o równaniach
są zawarte w prostych o równaniach 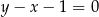 i
i 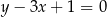 odpowiednio. Promień okręgu wpisanego w romb
odpowiednio. Promień okręgu wpisanego w romb 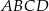 jest równy
jest równy 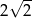 , a środek tego okręgu leży poniżej osi
, a środek tego okręgu leży poniżej osi 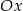 . Oblicz współrzędne punktu styczności okręgu wpisanego w romb
. Oblicz współrzędne punktu styczności okręgu wpisanego w romb 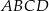 z jego bokiem
z jego bokiem 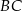 .
.

