/Szkoła średnia/Zadania maturalne/Matura 2023/Matura próbna
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis zadania.info poziom rozszerzony 4 marca 2023 Czas pracy: 180 minut
Dany jest nieskończony ciąg geometryczny 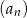 określony dla
określony dla 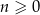 , którego iloraz jest równy
, którego iloraz jest równy 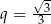 . Suma wszystkich wyrazów tego ciągu jest równa
. Suma wszystkich wyrazów tego ciągu jest równa 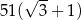 . Oblicz
. Oblicz 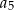 .
.
Napisz równanie stycznej do wykresu funkcji 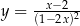 w punkcie
w punkcie 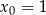 .
.
Wiedząc, że 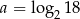 i
i 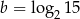 oblicz
oblicz 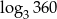 .
.
Wyznacz wszystkie wartości parametru 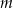 , dla których równanie
, dla których równanie
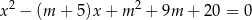
ma dwa różne rozwiązania rzeczywiste 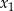 oraz
oraz 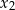 , spełniające warunek
, spełniające warunek
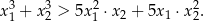
Udowodnij, że suma sześcianów trzech kolejnych liczb całkowitych nieparzystych jest podzielna przez 9.
Informacja do zadań 6.1 i 6.2
Funkcja 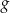 jest określona wzorem
jest określona wzorem 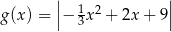 dla każdego
dla każdego 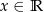 . Fragment wykresu funkcji
. Fragment wykresu funkcji 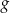 w kartezjańskim układzie współrzędnych
w kartezjańskim układzie współrzędnych 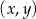 przedstawiono na rysunku (jednostki pominięto).
przedstawiono na rysunku (jednostki pominięto).
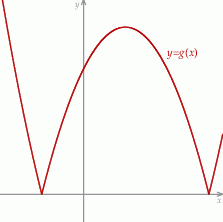
Wyznacz zbiór wszystkich wartości, jakie funkcja 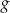 przyjmuje w przedziale
przyjmuje w przedziale ![[2,11]](https://img.zadania.info/zes/0081806/HzesT22x.gif) .
.
Wyznacz zbiór wszystkich wartości parametru 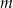 , dla których równanie
, dla których równanie 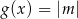 ma dokładnie dwa rozwiązania dodatnie.
ma dokładnie dwa rozwiązania dodatnie.
Rozwiąż równanie
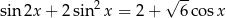
w przedziale ![[− π ,π]](https://img.zadania.info/zes/0081806/HzesT26x.gif) .
.
Podstawy trapezu 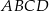 mają długości
mają długości 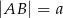 i
i 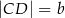 , przy czym
, przy czym 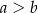 . Udowodnij, że odcinek łączący środki przekątnych tego trapezu ma długość
. Udowodnij, że odcinek łączący środki przekątnych tego trapezu ma długość 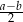 .
.
W pierwszej urnie umieszczono 3 kule białe i 5 kul czarnych, a w drugiej urnie 7 kul białych i 4 kule czarne. Losujemy jedną kulę z pierwszej urny i przekładamy ją do drugiej urny. Następnie losujemy dwie kule z urny drugiej. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że dwie kule wylosowane z drugiej urny są w różnych kolorach.
Punkty 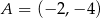 i
i 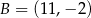 są wierzchołkami trójkąta
są wierzchołkami trójkąta 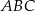 . Wierzchołek
. Wierzchołek 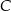 tego trójkąta leży na prostej
tego trójkąta leży na prostej 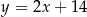 , a dwusieczna kąta
, a dwusieczna kąta 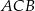 przecina bok
przecina bok 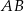 w punkcie
w punkcie 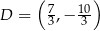 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 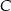 trójkąta
trójkąta 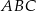 .
.
Rozpatrujemy wszystkie trójkąty równoramienne 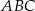 (
(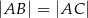 ), na których opisano okrąg o promieniu
), na których opisano okrąg o promieniu 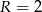 . Niech
. Niech 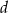 oznacza długość ramienia
oznacza długość ramienia 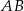 trójkąta.
trójkąta.
- Wykaż, że pole
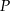 każdego z tych trójkątów, jako funkcja długości
każdego z tych trójkątów, jako funkcja długości 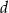 , wyraża się wzorem
, wyraża się wzorem 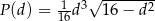 .
. - Wyznacz dziedzinę funkcji
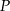 .
. - Oblicz długość ramienia
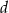 tego z rozpatrywanych trójkątów, który ma największe pole. Oblicz to największe pole.
tego z rozpatrywanych trójkątów, który ma największe pole. Oblicz to największe pole.
Krawędź boczna ostrosłupa prawidłowego trójkątnego jest nachylona do płaszczyzny podstawy pod kątem  . Przez krawędź podstawy tego ostrosłupa poprowadzono płaszczyznę, która jest nachylona do płaszczyzny podstawy pod katem
. Przez krawędź podstawy tego ostrosłupa poprowadzono płaszczyznę, która jest nachylona do płaszczyzny podstawy pod katem 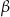 , i która przecina przeciwległą krawędź ostrosłupa (zobacz rysunek).
, i która przecina przeciwległą krawędź ostrosłupa (zobacz rysunek).
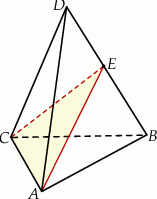
Oblicz stosunek pola powierzchni otrzymanego przekroju do pola powierzchni podstawy ostrosłupa jeżeli wiadomo, że 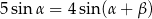 .
.

