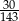Zadanie nr 1995360
Na stole leżało 14 banknotów: 2 banknoty o nominale 100 zł, 2 banknoty o nominale 50 zł i 10 banknotów o nominale 20 zł. Wiatr zdmuchnął na podłogę 5 banknotów. Oblicz prawdopodobieństwo tego, że na podłodze leży dokładnie 130 zł. Odpowiedź podaj w postaci ułamka nieskracalnego.
Rozwiązanie
Jak zwykle w zadaniach z prawdopodobieństwa najważniejszy jest wybór odpowiedniej przestrzeni 
zdarzeń elementarnych. Pierwszy pomysł mógłby być taki, że pojedyncze zdarzenie to nominały banknotów, które spadły na podłogę – to jednak prowadzi do kombinacji z powtórzeniami. Prościej (rachunkowo) jest jednak nie utożsamiać ze sobą banknotów o tych samych nominałach i za pojedyncze zdarzenie traktować wybór 5 banknotów z 14. W takim modelu
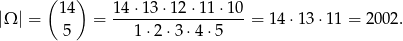
A jakie są zdarzenia sprzyjające? Chwila zastanowienia i jest jasne, że 130 zł można dostać tylko jako 50 zł+4
20 zł (nie może być wśród tych banknotów 100 zł, nie mogą być same 20 zł, nie może być dwóch 50 zł). Ile jest zdarzeń sprzyjających? 50 zł możemy wybrać na 2 sposoby, a 4 dwudziestki na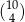 
sposobów, czyli razem mamy (twierdzenie o mnożeniu, lub zdrowy rozsądek):
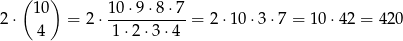
sposobów.
Szukane prawdopodobieństwo wynosi zatem:
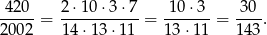
Odpowiedź: 
